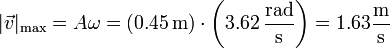Partícula suspendida de resorte y barra
De Laplace
Contenido |
1 Enunciado
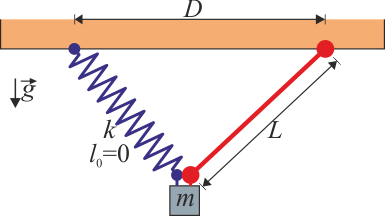
Una partícula de peso 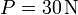 se encuentra atada simultáneamente a una barra rígida de longitud
se encuentra atada simultáneamente a una barra rígida de longitud 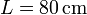 y a un muelle de longitud natural nula y constante
y a un muelle de longitud natural nula y constante 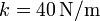 . Los anclajes de la barra y el resorte distan
. Los anclajes de la barra y el resorte distan 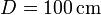 .
.
- Determine la posición de equilibrio de la masa. ¿Cuánto vale la tensión de la barra en este momento? ¿Cuál es la longitud del resorte?
- Suponga que se corta la unión de la masa con el resorte. ¿Qué tipo de movimiento describe la masa a partir de ese momento? Halle la rapidez máxima que alcanza.
- Suponga que, en lugar de lo anterior, se corta la unión de la masa con la barra. ¿Qué movimiento describe en ese caso? Calcule la amplitud y frecuencia del movimiento resultante. Halle la rapidez máxima que alcanza.
2 Posición de equilibrio
Según sea de grande la masa de la partícula, el resorte se estirará más o menos. La posición de equilibrio será aquella en que la suma de fuerzas sea igual a cero.
Sobre la masa actúan tres fuerzas: el peso, la tensión de la barra y la fuerza recuperadora del muelle, por lo que

Si consideramos el origen de coordenadas en el punto de anclaje del resorte, y el eje Z como el vertical hacia arriba, el peso tiene la expresión en la base cartesiana
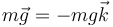
La fuerza recuperadora vale, puesto que la longitud en reposo del resorte es nula,
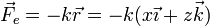
Hay que destacar que en esta expresión z será una cantidad negativa, pues el vector de posición apunta hacia el semiespacio z < 0
La tensión tiene módulo FT y va en la dirección de la barra. Si ésta forma un ángulo θ con la horizontal
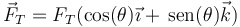
Llevando todo esto a la ecuación de equilibrio nos quedan las ecuaciones
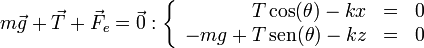
{}
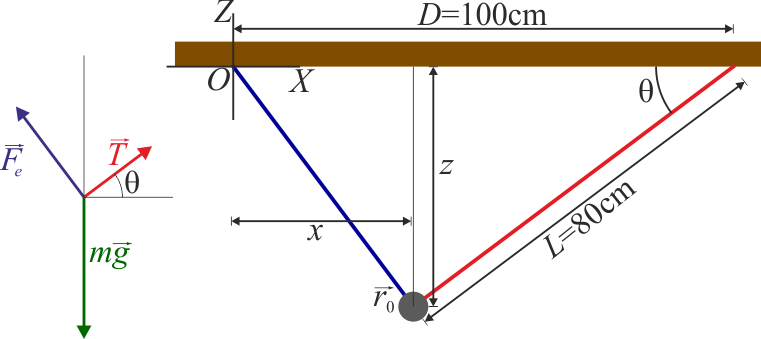
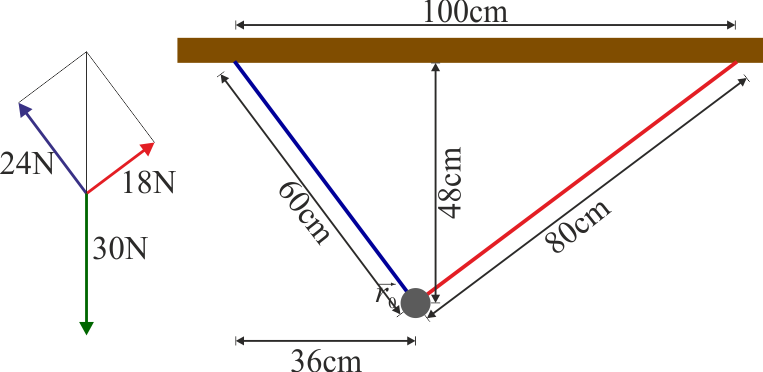
Tenemos dos ecuaciones pero cuatro incógnitas: x, z, θ y el módulo de la tensión, FT. Por ello, necesitamos dos ecuaciones adicionales. Esta nos las da el que los dos puntos de anclaje y la masa forman un triángulo de base D y altura h = | z | . De aquí

Despejando y sustituyendo en las ecuaciones de equilibrio

Dividiendo una ecuación por la otra obtenemos la inclinación de la barra
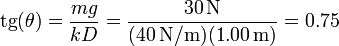
siendo el resto de las funciones trigonométricas

Una vez que tenemos este ángulo, tenemos la posición
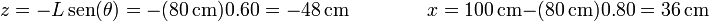
En forma vectorial
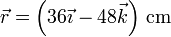
La longitud del resorte en la posición de equilibrio es
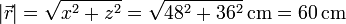
El módulo de la tensión de la barra en el equilibrio la calculamos empleando cualquiera de las componentes de la ecuación de movimiento.
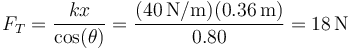
siendo su valor como vector
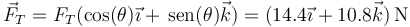
Podemos hallar también la fuerza que ejerce el muelle y su módulo
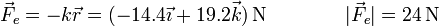
Vemos que la suma vectorial de la tensión y la fuerza recuperadora iguala al peso (no así, por supuesto, la suma de sus módulos).
3 Partícula sujeta a la barra
Una vez que se libera del resorte, el sistema se convierte en un péndulo simple, en el que la masa puede oscilar suspendida de la barra de longitud L. Su posición inicial es la de equilibrio calculada en el apartado anterior y su velocidad es nula, pues se encontraba en reposo.
La rapidez máxima la alcanza cuando pasa por el punto más bajo y la barra es vertical. Tal como se calcula en el problema de la rapidez y tensión de un péndulo, esta rapidez equivale a la de una masa que cayera por acción de la gravedad

siendo h la diferencia en altura entre el punto inicial y el punto inferior. En este caso este desnivel vale
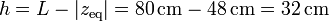
por lo que la celeridad máxima es
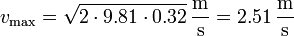
4 Partícula sujeta al resorte
Si lo que se libera es la barra, la masa comienza a moverse por la acción combinada del peso y la fuerza recuperadora del muelle. La intuición nos sugiere que describirá una oscilación en arco, similar a un péndulo. Sin embargo, no es eso lo que resulta de las ecuaciones de movimiento. La partícula está gobernada por
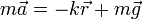
que podemos reescribir como
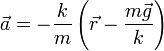
Esta es la ecuación de un oscilador armónico de frecuencia

y punto de equilibrio

La posición inicial de la partícula es la de equilibrio calculada en el primer apartado
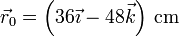
La velocidad inicial es nula. Por tanto, la masa describe un movimiento armónico simple, rectilíneo, con posición inicial la indicada y con punto central el de equilibrio del oscilador armónico.
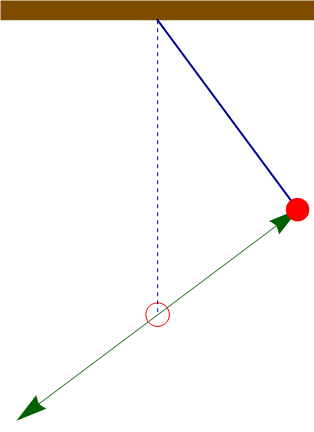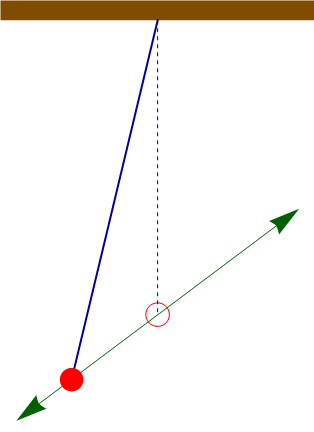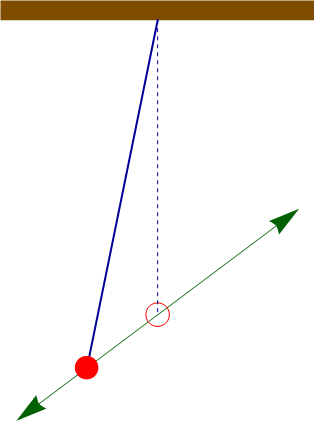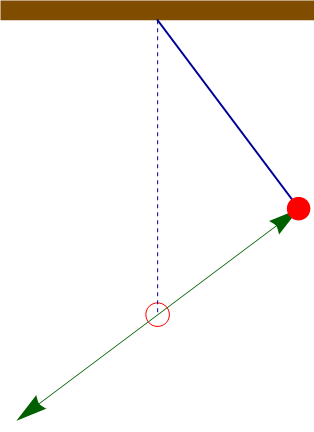
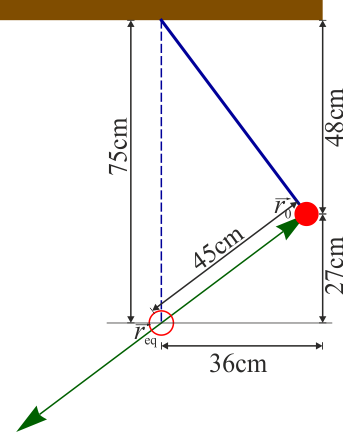
La amplitud de las oscilaciones la da la distancia entre el punto inicial y el de equilibrio
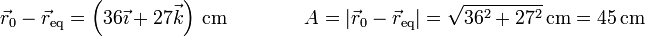
La máxima rapidez se alcanza cuando el oscilador pasa por el punto de equilibrio. Podemos hallar esta rapidez empleando la ley de conservación de la energía. Inicialmente (justo tras cortar la unión con la barra) posee una energía mecánica
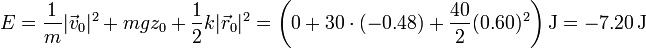
Cuando pasa por el punto de equilibrio, la energía mecánica es
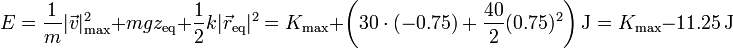
Igualando y despejando obtenemos la energía cinética máxima
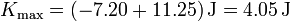
Podíamos haber obtenido esta energía cinética máxima directamente del movimiento de un oscilador armónico

A partir de la energía cinética hallamos la rapidez máxima
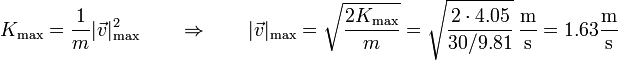
También puede hallarse esta rapidez máxima a partir de las ecuaciones del movimiento armónico simple