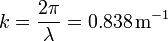Onda electromagnética con polarización lineal GIA
De Laplace
Contenido |
1 Enunciado
El campo eléctrico de una onda electromagnética plana es 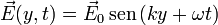 , con
, con 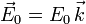 (E0 es positivo). La frecuencia de la onda es
(E0 es positivo). La frecuencia de la onda es 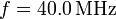 y el valor máximo del campo eléctrico es
y el valor máximo del campo eléctrico es 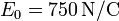 .
.
- ¿Cuál es la dirección y sentido de propagación de la onda?
- ¿Cómo es el campo magnético de la onda?
- ¿Cuánto vale la longitud de onda, el número de onda y el período de la onda?
2 Solución
2.1 Dirección y sentido de propagación
De la fase en la expresión del campo eléctrico vemos que la dirección de propagación de la onda es el eje Y y el sentido es el negativo del eje Y. Es decir, el vector unitario que indica la dirección y sentido de propagación de la onda es
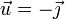
2.2 Campo magnético
Al ser una onda plana, el campo magnético ha de ser perpendicular al campo eléctrico y a la dirección de propagación. Como el enunciado nos dice que el campo es paralelo al vector  y del apartado anterior sabemos que la dirección de propagación es la del eje Y, el campo magnético ha de ser de la forma
y del apartado anterior sabemos que la dirección de propagación es la del eje Y, el campo magnético ha de ser de la forma
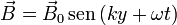
con 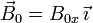 .
El signo de B0x se obtiene del hecho de que el producto vectorial
.
El signo de B0x se obtiene del hecho de que el producto vectorial 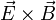 ha de ser paralelo a
ha de ser paralelo a  . Entonces
. Entonces
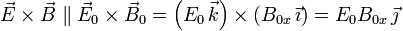
Debe cumplirse 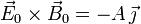 con A positivo. Por tanto
con A positivo. Por tanto
B0x = − B0
con B0 positivo. El campo magnético es
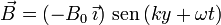
El módulo del campo magnético es
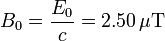
2.3 Longitud de onda, número de onda y período
El período de la onda es

La longitud de onda es
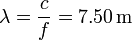
Y el número de onda es