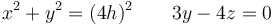Ejemplo de movimiento armónico tridimensional
De Laplace
Contenido |
1 Enunciado
Una partícula se mueve de forma que en todo momento verifica la ecuación del oscilador armónico en tres dimensiones
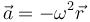
siendo su posición y velocidad iniciales

- Calcule la posición, velocidad y aceleración de la partícula en todo instante.
- Para el instante t = 0 halle:
- El triedro de Frenet:
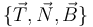 .
.
- Las componentes intrínsecas de la aceleración (en forma escalar y vectorial).
- La posición del centro de curvatura.
- El triedro de Frenet:
- Empleando coordenadas cilíndricas y su base asociada:
- Escriba las ecuaciones horarias
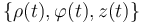 .
.
- Escriba los vectores de posición, velocidad y aceleración como función del tiempo.
- Escriba las ecuaciones horarias
- Identifique este movimiento: ¿Es plano? ¿Es rectilíneo? ¿Es uniforme? ¿Cómo es la trayectoria? Justifique las respuestas.
2 Posición, velocidad y aceleración
2.1 Posición
En un oscilador armónico tridimensional, la solución general para la posición es de la forma
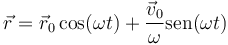
Sustituimos los datos del enunciado y queda
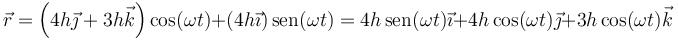
2.2 Velocidad
Una vez que tenemos la posición instantánea, calculamos la velocidad instantánea derivando respecto al tiempo
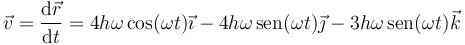
2.3 Aceleración
Para hallar la aceleración podemos derivar de nuevo o usar la ecuación del oscilador armónico
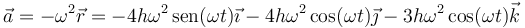
3 Estado en t=0
Para analizar el estado en t = 0 no necesitamos el apartado anterior, ya que el enunciado nos da la posición
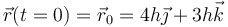
la velocidad
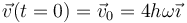
y la aceleración
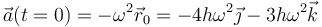
3.1 Triedro de Frenet
3.1.1 Vector tangente
Es el unitario en la dirección y sentido de la velocidad
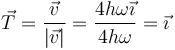
3.1.2 Vector normal
Es el unitario en la dirección y sentido de la aceleración normal. En este instante tenemos que la aceleración es perpendicular a la velocidad
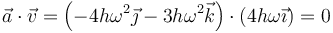
por lo que toda la aceleración es normal, siendo su módulo
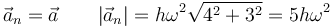
lo que da el vector normal
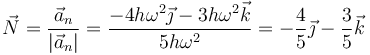
3.1.3 Vector binormal
Es el producto vectorial de los dos anteriores
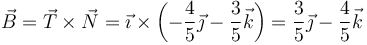
También podía hallarse directamente como
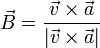
3.2 Componentes de la aceleración
3.2.1 Tangencial
Según hemos visto, en este instante la aceleración es ortogonal a la velocidad, por lo que no tiene componente tangencial

3.2.2 Normal
Al ser nula la aceleración tangencial en este instante, la aceleración normal es toda la aceleración
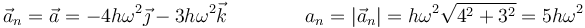
3.3 Radio y centro de curvatura
El radio de curvatura en este instante es igual a
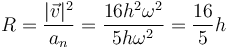
y el centro de curvatura
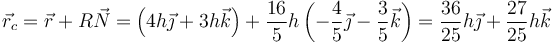
4 Expresión en cilíndricas
4.1 Coordenadas
Si separamos la posición instantánea en sus componentes cartesianas nos queda
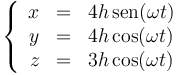
La coordenada radial ρ es la distancia al eje Z
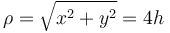
Esta distancia es constante, ya que la proyección en el plano XY describe un movimiento circular.
Para la coordenada acimutal tenemos
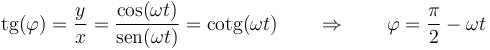
ya que la cotangente es la tangente del complementario.
Por último la coordenada vertical es la misma que en cartesianas
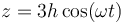
Inversamente, el paso de cilíndricas a cartesianas es
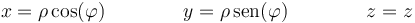
y comparando esta expresión con la de este movimiento concreto es claro que la coordenada radial es constante y que el ángulo  va como el complementario de ωt (ya que se intercambia el seno por el coseno).
va como el complementario de ωt (ya que se intercambia el seno por el coseno).
4.2 Vectores
4.2.1 Posición
La expresión del vector de posición en cilíndricas es
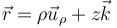
que en este caso queda
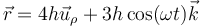
4.2.2 Velocidad
La expresión para la velocidad es
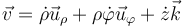
que en este caso, al ser la coordenada radial constante
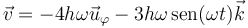
4.2.3 Aceleración
Recurriendo de nuevo a la ecuación del oscilador armónico nos ahorramos escribir la expresión general en cilíndricas.
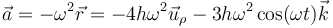
5 Descripción del movimiento
Este es un movimiento plano, ya que se puede escribir como combinación lineal de dos vectores
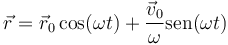
No es rectilíneo ya que según hemos visto su aceleración normal no es nula.
Tampoco es uniforme, ya que su rapidez no es constante. Si hallamos esta en general queda
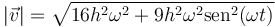
La forma de la trayectoria es una elipse como corresponde a la solución general del oscilador armónico tridimensional
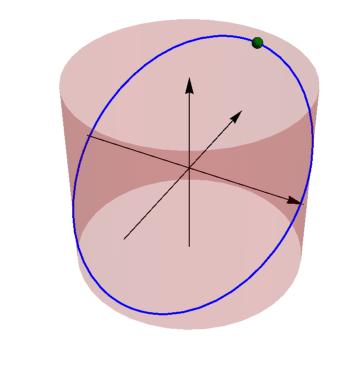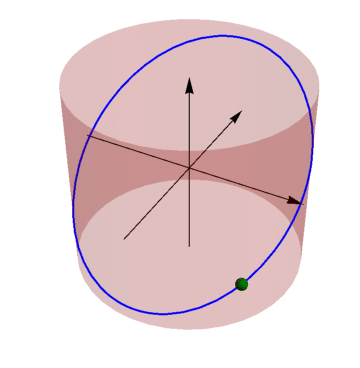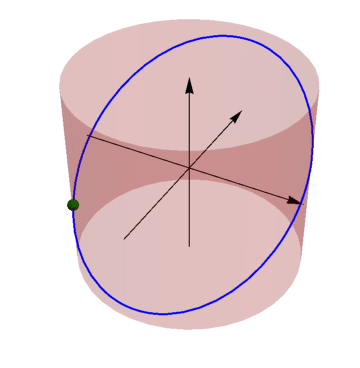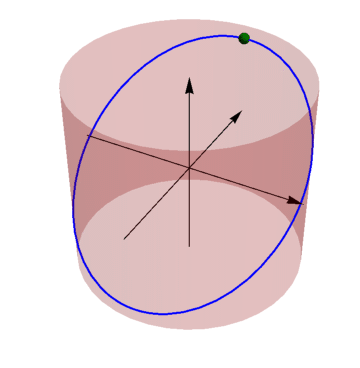
Se puede ver también que es una elipse porque se trata de la intersección de un cilindro con un plano oblícuo