Calor en una expansión isoterma por un peso

De Laplace

Contenido

1 Enunciado
2 Descenso del pistón
3 Calor en el descenso
4 Calor en el ascenso
5 Producción de entropía

1 Enunciado

Se tiene una balanza formada por un recipiente cilíndrico de 16 cm² de sección lleno de aire (considerado como un gas ideal). El tubo está cerrado herméticamente en su parte inferior por un émbolo que puede deslizarse sin rozamiento y que tiene un gancho en su cara inferior. Las paredes y el émbolo no están aislados térmicamente. Inicialmente el émbolo se encuentra a 15 cm de la pared superior, y el gas en equilibrio mecánico y térmico con el exterior, que se halla a 1 bar y 300 K. Se cuelga bruscamente del pistón un saco de harina de 4 kg.

¿Cuánto desciende aproximadamente el pistón hasta que se alcanza de nuevo el equilibrio?
¿Cuánto vale aproximadamente el calor que entra en el sistema en este proceso?
Suponga que el saco tiene un agujero, de forma que la harina se escapa lentamente hasta vaciarse por completo (despreciamos el peso del propio saco). ¿Cuánto vale el calor que entra en el sistema en este segundo proceso?

Datos: Constante de los gases ideales: 8.314 J/K·mol; Razón de capacidades caloríficas del aire: 1.4.

2 Descenso del pistón

Este problema es muy similar al la compresión por un peso, que se analiza en este problema y este problema, con la diferencia de que en este caso la pesa reduce la presión en lugar de aumentarla. Tenemos inicialmente un cilindro que contiene un gas con presión volumen y temperatura:

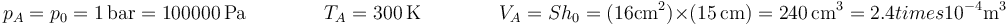
$p_A = p_0=1\,\mathrm{bar} = 100000\,\mathrm{Pa}\qquad\qquad T_A = 300\,\mathrm{K}\qquad\qquad V_A = S h_0 = (16\mathrm{cm}^2)\times(15\,\mathrm{cm})=240\,\mathrm{cm}^3=2.4ºtimes 10^{-4}\mathrm{m}^3$

Cuando se cuelga el saco, la presión externa se reduce en la cantidad correspondiente al peso

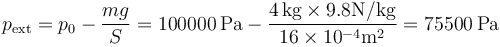
$p_\mathrm{ext} = p_0-\frac{mg}{S}= 100000\,\mathrm{Pa}-\frac{4\,\mathrm{kg}\times 9.8\mathrm{N}/\mathrm{kg}}{16\times 10^{-4}\mathrm{m}^2}=75500\,\mathrm{Pa}$

El nuevo estado de equilibrio se alcanza cuando la presión interior iguala a la nueva presión externa, siendo la temperatura final igual a la inicial, por no estar el sistema aislado térmicamente.

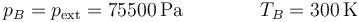
$p_B = p_\mathrm{ext}=75500\,\mathrm{Pa}\qquad\qquad T_B = 300\,\mathrm{K}$

Aplicando la ley de Boyle obtenemos el nuevo volumen

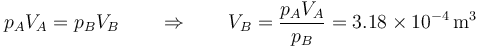
$p_AV_A=p_BV_B\qquad\Rightarrow\qquad V_B = \frac{p_AV_A}{p_B}=3.18\times 10^{-4}\,\mathrm{m}^3$

y la nueva distancia del pistón, dividiendo por la sección del tubo

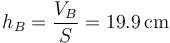
$h_B = \frac{V_B}{S}= 19.9\,\mathrm{cm}$

con lo que el descenso del pistón vale

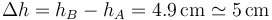
$\Delta h =h_B-h_A=4.9\,\mathrm{cm}\simeq 5\,\mathrm{cm}$

3 Calor en el descenso

En este descenso la temperatura final es la misma que la inicial (puede que las intermedias no lo sean, o ni siquiera existir). Al ser el aire un gas aproximadamente ideal su energía interna depende exclusivamente de su temperatura

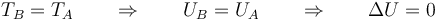
$T_B = T_A \qquad\Rightarrow\qquad U_B = U_A \qquad\Rightarrow\qquad \Delta U = 0$

y, por el primer principio de la termodinámica

$0 = \Delta U = Q + W \qquad\Rightarrow\qquad Q = -W$

Para hallar el calor debemos calcular el trabajo sobre en el sistema, según la expresión general

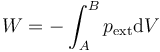
$W = -\int_A^B p_\mathrm{ext}\mathrm{d}V$

En el descenso la presión exterior es constante, ya que una vez que se cuelga el saco, este ejerce una fuerza constante sobre el émbolo (suponemos que no le da tiempo a vaciarse apreciablemente). Por tanto, el cálculo es trivial

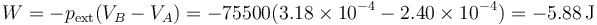
$W = -p_\mathrm{ext}(V_B-V_A) = -75500(3.18\times 10^{-4}-2.40\times10^{-4}) = -5.88\,\mathrm{J}$

El trabajo es negativo ya que realmente lo realiza el sistema sobre el ambiente al expandirse. El calor será igual, pero cambiado de signo

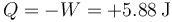
$Q=-W = +5.88\,\mathrm{J}$

4 Calor en el ascenso

A medida que la harina va cayendo del saco va disminuyendo la fuerza que tira hacia abajo por lo que la presión sobre el gas se incrementa y el pistón vuelve a subir. El estado final es el mismo que teníamos al principio, con el pistón a 15cm de la parte superior y la presión y la temperatura iniciales.

Por ser la temperatura final igual a la inicial de nuevo se cumple

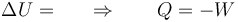
$\Delta U = \qquad\Rightarrow\qquad Q = -W$

Este proceso no es el inverso del del apartado anterior. El descenso es un proceso no cuasiestático en el que la presión exterior permanece constante. El ascenso es cuasiestático y en él la presión varía progresivamente.

Al ir cayendo poco a poco podemos suponer que el aire interior está siempre en equilibrio con el exterior y a la misma temperatura de 300K. Por estar en equilibrio mecánico, en todo momento la presión interior coincide con la exterior

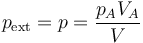
$p_\mathrm{ext}=p=\frac{p_AV_A}{V}$

Llevando esto a la integral

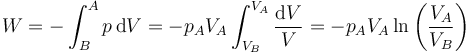
$W = -\int_B^A p\,\mathrm{d}V = -p_AV_A\int_{V_B}^{V_A}\frac{\mathrm{d}V}{V}=-p_AV_A\ln\left(\frac{V_A}{V_B}\right)$

Numéricamente

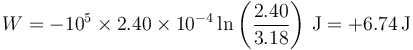
$W = -10^5\times 2.40\times 10^{-4}\ln\left(\frac{2.40}{3.18}\right)\,\mathrm{J}=+6.74\,\mathrm{J}$

Este trabajo es positivo porque al comprimirse el aire se realiza trabajo sobre el sistema. El calor será entonces, negativo, ya que sale del sistema

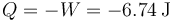
$Q = -W = -6.74\,\mathrm{J}$

5 Producción de entropía

El proceso de subida es uno cuasiestático e isotermo. Esto quiere decir que el proceso es reversible. Si en un momento dado dejara de caer harina y en su lugar empezara a añadirse harina nueva progresivamente, el pistón volvería a bajar gradualmente.

Por tanto, la variación de entropía del universo en este proceso es igual a cero

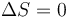
$\Delta S = 0\,$

Esto no implica que la variación de entropía del sistema y del entorno sean nulas. Solo que son iguales y opuestas. La del sistema disminuye y la del ambiente aumenta. El cálculo es análogo de otro problema.

Calor en una expansión isoterma por un peso

De Laplace

Contenido

1 Enunciado

2 Descenso del pistón

3 Calor en el descenso

4 Calor en el ascenso

5 Producción de entropía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES