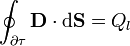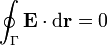Vector desplazamiento
De Laplace
Contenido |
1 Ecuaciones de la electrostática en dieléctricos
Cuando se tienen en cuenta las densidades de carga de polarización las ecuaciones de la electrostática se escriben
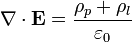
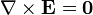
siendo
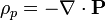
la densidad volumétrica de carga de polarización y ρl la densidad volumétrica de carga libre, esto es, aquella que no está asociada a la polarización del material.
En forma integral estas ecuaciones se escriben
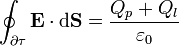
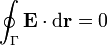
siendo Qp y Ql la carga total de polarización y libre contenida en el volumen τ.
Cuando tanto las densidades de carga libre como la polarización del medio son cantidades conocidas, estas ecuaciones (junto con las correspondientes condiciones de salto y de contorno) permiten determinar completamente el campo eléctrico.
Sin embargo, lo habitual es que la polarización de un material no sea conocida de antemano, sino que sea provocada por la acción del campo eléctrico sobre el material (induciendo dipolos o rotando los ya existentes). Así pues, el campo eléctrico es simultáneamente causa y efecto de la polarización. En términos matemáticos, esto significa que las ecuaciones escritas arriba no son completas pues tanto  como ρp son cantidades desconocidas.
como ρp son cantidades desconocidas.
Podemos eliminar formalmente la densidad de carga de polarización observando que la ley de Gauss se puede transformar de la manera siguiente:
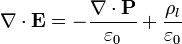

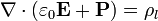
Si llamamos
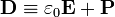
la ley de Gauss queda simplemente
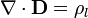
A este campo vectorial  se le denomina vector desplazamiento.
se le denomina vector desplazamiento.
2 Definición del vector desplazamiento
Se define el vector desplazamiento eléctrico,  , mediante la ecuación
, mediante la ecuación
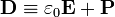
El desplazamiento eléctrico es un campo vectorial que puede definirse en todos los puntos del espacio. En las regiones donde no haya medios materiales y por tanto la polarización sea nula, el desplazamiento es simplemente
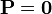

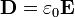
De la definición se deduce que el vector desplazamiento tiene las mismas unidades que la polarización, esto es, se mide en C/m² (tiene unidades de densidad superficial de carga).
2.1 Fuentes del vector desplazamiento
Como todos los campos vectoriales, el vector desplazamiento posee tanto fuentes escalares como vectoriales
2.1.1 Fuentes escalares
Según hemos visto antes
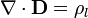
es decir, las fuentes escalares de  son las densidades de carga libre.
son las densidades de carga libre.
2.1.2 Fuentes vectoriales
Tomando el rotacional en la definición
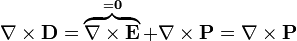
hemos aplicado que el rotacional del campo eléctrico es cero, lo cual es cierto solo en electrostática. En situaciones dependientes del tiempo habrá que modificar esta ecuación.
Este resultado implica que el vector desplazamiento no es un campo irrotacional, como el campo electrostático (ni tampoco solenoidal). Posee fuentes vectoriales dependientes de la polarización, que por tanto no ha desaparecido del sistema, sino que ahora aparece en otro punto de las ecuaciones.
3 Ecuaciones en función de E y D
En lugar de usar las ecuaciones en términos exclusivamente del campo eléctrico o del vector desplazamiento, podemos escribir las ecuaciones de la electrostática en una forma mixta, más sencilla:
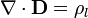

y en forma integral