Triángulo con muelle y rozamiento
De Laplace
Revisión a fecha de 16:54 25 ene 2010; Pedro (Discusión | contribuciones)
1 Enunciado
(Primer Parcial, Enero 2010, P1)
En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco
de radio R (sólido "0") rueda sin deslizar sobre el sólido "1". El centro del
disco, C, se desplaza con una velocidad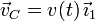 
. La barra de longitud 3R
(sólido "2") tiene su extremo C articulado en el centro del disco, mientras que se
apoya en el borde O del sólido "1".
- Determina gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}.
- En el instante en que la distancia entre los puntos O y B es igual a R, la velocidad del punto C es
. Calcula las reducciones cinemáticas de los tres movimientos en el punto C.
- Expresa el vector de posición del punto A en el sistema "1",
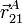, en función de un ángulo β arbitrario.
- Si
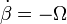, con Ω constante y positiva, calcula 
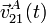y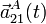 
para todo instante de tiempo en función de β, Ω y R.
