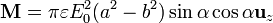Partícula elíptica en campo eléctrico oblicuo

De Laplace

Revisión a fecha de 13:35 13 ene 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Planteamiento
2 Coordenadas elípticas
3 Solución para el potencial
4 Momento dipolar
5 Torque
6 A partir del tensor de tensiones

1 Planteamiento

Tenemos una elipse de semiejes $a$ y $b$ ( $a > b$ ) recubierta de una capa doble. La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo $α$ con el semieje mayor.

El problema del potencial se convierte en la solución de la ecuación de Laplace

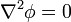
$\nabla^2\phi = 0$

con la condición de Neumann en la superficie de la partícula

$\mathbf{n}\cdot\nabla\phi = 0\qquad(\mathbf{r}\in S)$

y con el comportamiento asintótico

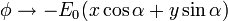
$\phi\to -E_0(x\cos\alpha+y\sin\alpha)\,$

2 Coordenadas elípticas

Para resolver el problema eléctrico empleamos las coordenadas elípticas definidas por

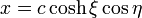
$x = c \cosh\xi\cos\eta\,$ $y = c \sinh\xi\sin\eta\,$

con

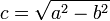
$c = \sqrt{a^2-b^2}$

En estas coordenadas la superficie de la elipse viene definida por

$\xi=\xi_0=\,\mathrm{arctanh}\left(\frac{b}{a}\right)$

Para estas coordenadas tenemos los factores de escala

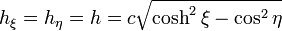
$h_\xi = h_\eta = h = c\sqrt{\cosh^2\xi-\cos^2\eta}$

Al ser iguales, la ecuación de Laplace preseva su forma, de manera que hay que resolver

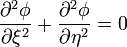
$\frac{\partial^2\phi}{\partial\xi^2}+\frac{\partial^2\phi}{\partial\eta^2}=0$

con la condición de Neumann

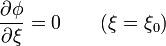
$\frac{\partial\phi}{\partial\xi}=0\qquad(\xi=\xi_0)\,$

y con la condición de que en el infinito

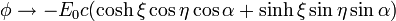
$\phi\to-E_0c(\cosh\xi\cos\eta\cos\alpha+\sinh\xi\sin\eta\sin\alpha)\,$

3 Solución para el potencial

La solución se halla simplemente observando que la condición de que a grandes distancias

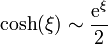
$\cosh(\xi)\sim \frac{\mathrm{e}^\xi}{2}$ $\sinh(\xi)\sim \frac{\mathrm{e}^\xi}{2}$

lo que nos permite sustituir el potencial en el infinito por

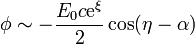
$\phi\sim -\frac{E_0c\mathrm{e}^{\xi}}{2}\cos(\eta-\alpha)$

y esta, que ya es de por sí una solución de la ecuación de Laplace, nos dice cual es la solución del problema completo (que en 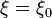$\xi = \xi_0\,$ tiene derivada nula). El potencial es

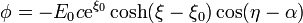
$\phi= -E_0c\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)\cos(\eta-\alpha)$

mientras que la función corriente, que nos da las líneas de campo, es

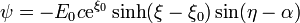
$\psi = -E_0c\mathrm{e}^{\xi_0}\sinh(\xi-\xi_0)\sin(\eta-\alpha)$

4 Momento dipolar

Para ver que esto equivale a un campo uniforme más un dipolo tenemos que demostrar que su comportamiento en puntos alejados va como

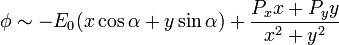
$\phi \sim -E_0(x\cos\alpha+y\sin\alpha) + \frac{P_xx+P_y y}{x^2+y^2}$

Para ello, en primer lugar, restamos el comportamiento asintótico

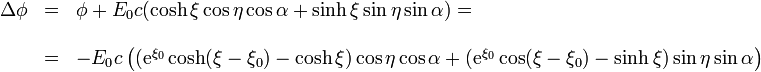
$\begin{array}{rcl}\Delta\phi & = & \phi + E_0 c(\cosh\xi\cos\eta\cos\alpha+\sinh\xi\sin\eta\sin\alpha)= \\ & & \\ & = & -E_0c\left((\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)-\cosh\xi)\cos\eta\cos\alpha+(\mathrm{e}^{\xi_0}\cos(\xi-\xi_0)-\sinh\xi)\sin\eta\sin\alpha\right)\end{array}$

Analizando los dos factores tenemos

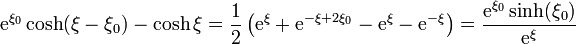
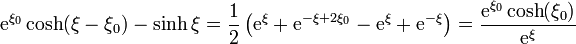
$\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)-\cosh\xi = \frac{1}{2}\left(\mathrm{e}^{\xi}+\mathrm{e}^{-\xi+2\xi_0}-\mathrm{e}^{\xi}-\mathrm{e}^{-\xi}\right) = \frac{\mathrm{e}^{\xi_0}\sinh(\xi_0)}{\mathrm{e}^{\xi}}$ $\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)-\sinh\xi = \frac{1}{2}\left(\mathrm{e}^{\xi}+\mathrm{e}^{-\xi+2\xi_0}-\mathrm{e}^{\xi}+\mathrm{e}^{-\xi}\right) = \frac{\mathrm{e}^{\xi_0}\cosh(\xi_0)}{\mathrm{e}^{\xi}}$

y por tanto

$\Delta\phi = -\frac{E_0c\mathrm{e}^{\xi_0}}{\mathrm{e}^\xi}\left(\sinh\xi_0\cos\eta\cos\alpha+\cosh\xi_0\sin\eta\sin\alpha\right)$

Para ver que esto es el potencial de una línea bifilar, observamos que para $ξ$ grande se cumple

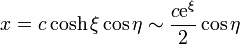
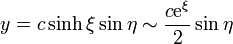
$x = c \cosh\xi\cos\eta \sim \frac{c\mathrm{e}^\xi}{2}\cos\eta$ $y = c \sinh\xi\sin\eta \sim \frac{c\mathrm{e}^\xi}{2}\sin\eta$

por lo que, en este mismo límite

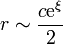
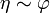
$r\sim \frac{c\mathrm{e}^\xi}{2}$ $\eta\sim\varphi$

lo que nos permite escribir el potencial residual en la forma asintótica

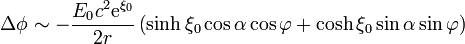
$\Delta\phi\sim -\frac{E_0c^2\mathrm{e}^{\xi_0}}{2r}\left(\sinh\xi_0\cos\alpha\cos\varphi+\cosh\xi_0\sin\alpha\sin\varphi\right)$

Podemos poner esta expresión en función de los datos originales observando que

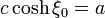
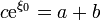
$c\cosh\xi_0=a\,$ $c\sinh\xi_0=b\,$ $c\mathrm{e}^{\xi_0}=a+b\,$

y queda

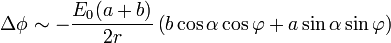
$\Delta\phi\sim -\frac{E_0(a+b)}{2r}\left(b\cos\alpha\cos\varphi+a\sin\alpha\sin\varphi\right)$

Comparando esto con el potencial de una línea bifilar de momento 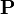$\mathbf{P}$ por unidad de longitud

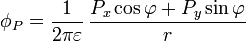
$\phi_P = \frac{1}{2\pi\varepsilon}\,\frac{P_x\cos\varphi+P_y\sin\varphi}{r}$

obtenemos que el momento dipolar visto desde el infinito es

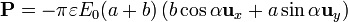
$\mathbf{P}=-\pi\varepsilon E_0(a+b)\left(b\cos\alpha\mathbf{u}_x+a\sin\alpha\mathbf{u}_y\right)$

5 Torque

Una vez que tenemos el momento dipolar y el campo aplicado, hallamos el par por unidad de longitud como

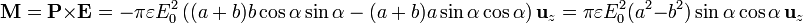
$\mathbf{M}=\mathbf{P}\times\mathbf{E}=-\pi\varepsilon E_0^2\left((a+b)b\cos\alpha\sin\alpha-(a+b)a\sin\alpha\cos\alpha\right)\mathbf{u}_z =\pi\varepsilon E_0^2(a^2-b^2)\sin\alpha\cos\alpha\,\mathbf{u}_z$

6 A partir del tensor de tensiones

El torque también debe poder calcularse a partir del flujo de $\mathbf{r}\times\mathsf{T}^e$ a través de una superficie que envuelva la partícula.

Considerando una superficie elíptica infinitamente próxima a la partícula se tiene que en ella

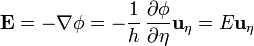
$\mathbf{E}=-\nabla\phi = -\frac{1}{h}\,\frac{\partial\phi}{\partial\eta}\mathbf{u}_\eta = E\mathbf{u}_\eta$

y el tensor de tensiones en esta superficie es

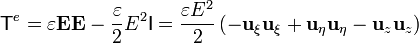
$\mathsf{T}^e=\varepsilon\mathbf{E}\mathbf{E}-\frac{\varepsilon}{2}E^2\mathsf{I}=\frac{\varepsilon E^2}{2}\left(-\mathbf{u}_\xi\mathbf{u}_\xi+\mathbf{u}_\eta\mathbf{u}_\eta-\mathbf{u}_z\mathbf{u}_{z}\right)$

El diferencial de superficie (por unidad de longitud vertical) es

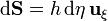
$\mathrm{d}\mathbf{S}=h\,\mathrm{d}\eta\,\mathbf{u}_\xi$

con lo que la contracción 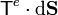$\mathsf{T}^e\cdot\mathrm{d}\mathbf{S}$ vale

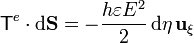
$\mathsf{T}^e\cdot\mathrm{d}\mathbf{S} = -\frac{h\varepsilon E^2}{2}\,\mathrm{d}\eta\,\mathbf{u}_\xi$

El vector de posición, en coordenadas elípticas, es

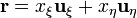
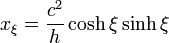
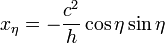
$\mathbf{r}=x_\xi\mathbf{u}_\xi+x_\eta\mathbf{u}_\eta\,$ $x_\xi=\frac{c^2}{h}\cosh\xi\sinh\xi$ $x_\eta =-\frac{c^2}{h}\cos\eta\sin\eta$

Multiplicando vectorialmente

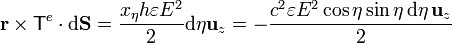
$\mathbf{r}\times\mathsf{T}^e\cdot\mathrm{d}\mathbf{S}=\frac{x_\eta h \varepsilon E^2}{2}\mathrm{d}\eta\mathbf{u}_z=-\frac{c^2\varepsilon E^2 \cos\eta\sin\eta\,\mathrm{d}\eta\,\mathbf{u}_z}{2}$

El valor de $E$ en la elipse es

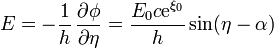
$E = -\frac{1}{h}\,\frac{\partial \phi}{\partial \eta} = \frac{E_0c\mathrm{e}^{\xi_0}}{h}\sin(\eta-\alpha)$

lo que nos da la integral para el momento

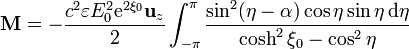
$\mathbf{M}=-\frac{c^2\varepsilon E_0^2\mathrm{e}^{2\xi_0}\mathbf{u}_z}{2}\int_{-\pi}^\pi \frac{\sin^2(\eta-\alpha)\cos\eta\sin\eta\,\mathrm{d}\eta}{\cosh^2\xi_0-\cos^2\eta}$

Desarrollando $sin 2 (η - α)$

$\sin^2(\eta-\alpha) = \sin^2\eta\cos^2\alpha+\cos^2\eta\sin^2\alpha-2\sin\eta\cos\eta\sin\alpha\cos\alpha\,$

Los dos primeros términos, al integrarlos, dan cero, por tratarse de un integrando impar sobre un intervalo par. Queda entonces

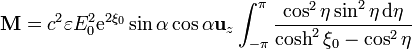
$\mathbf{M}=c^2\varepsilon E_0^2\mathrm{e}^{2\xi_0}\sin\alpha\cos\alpha\mathbf{u}_z\int_{-\pi}^\pi \frac{\cos^2\eta\sin^2\eta\,\mathrm{d}\eta}{\cosh^2\xi_0-\cos^2\eta}$

Esta integral se puede hacer, por ejemplo, por residuos (o usando el Mathematica), y sale

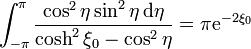
$\int_{-\pi}^\pi \frac{\cos^2\eta\sin^2\eta\,\mathrm{d}\eta}{\cosh^2\xi_0-\cos^2\eta} =\pi \mathrm{e}^{-2\xi_0}$

así que obtenemos finalmente

$\mathbf{M}=\pi \varepsilon E_0^2(a^2-b^2)\sin\alpha\cos\alpha\mathbf{u}_z$

Partícula elíptica en campo eléctrico oblicuo

De Laplace

Contenido

1 Planteamiento

2 Coordenadas elípticas

3 Solución para el potencial

4 Momento dipolar

5 Torque

6 A partir del tensor de tensiones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES