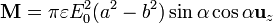Partícula elíptica en campo eléctrico oblicuo

De Laplace

Contenido

1 Planteamiento
2 Coordenadas elípticas
3 Solución para el potencial
4 Momento dipolar
5 Torque
6 A partir del tensor de tensiones

1 Planteamiento

Tenemos una elipse de semiejes $a$ y $b$ ( $a > b$ ) en el seno de un electrolito recubierta de una capa doble (partícula perfectamente polarizable). La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo $α$ con el semieje mayor. Este sistema es equivalente al de una partícula aislante inmersa en un medio conductor óhmico.

El problema del potencial se convierte en la solución de la ecuación de Laplace

$\nabla^2\phi = 0$

con la condición de Neumann en la superficie de la partícula

$\mathbf{n}\cdot\nabla\phi = 0\qquad(\mathbf{r}\in S)$

y con el comportamiento asintótico

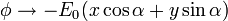
$\phi\to -E_0(x\cos\alpha+y\sin\alpha)\,$

2 Coordenadas elípticas

Para resolver el problema eléctrico empleamos las coordenadas elípticas definidas por

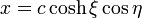
$x = c \cosh\xi\cos\eta\,$ $y = c \sinh\xi\sin\eta\,$

con

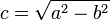
$c = \sqrt{a^2-b^2}$

En estas coordenadas la superficie de la elipse viene definida por

$\xi=\xi_0=\,\mathrm{arctanh}\left(\frac{b}{a}\right)$

Para estas coordenadas tenemos los factores de escala

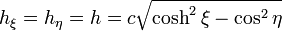
$h_\xi = h_\eta = h = c\sqrt{\cosh^2\xi-\cos^2\eta}$

Al ser iguales, la ecuación de Laplace preseva su forma, de manera que hay que resolver

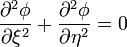
$\frac{\partial^2\phi}{\partial\xi^2}+\frac{\partial^2\phi}{\partial\eta^2}=0$

con la condición de Neumann

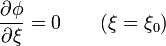
$\frac{\partial\phi}{\partial\xi}=0\qquad(\xi=\xi_0)\,$

y con la condición de que en el infinito

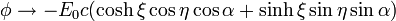
$\phi\to-E_0c(\cosh\xi\cos\eta\cos\alpha+\sinh\xi\sin\eta\sin\alpha)\,$

3 Solución para el potencial

La solución se halla simplemente observando que la condición de que a grandes distancias

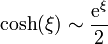
$\cosh(\xi)\sim \frac{\mathrm{e}^\xi}{2}$ $\sinh(\xi)\sim \frac{\mathrm{e}^\xi}{2}$

lo que nos permite sustituir el potencial en el infinito por

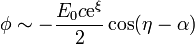
$\phi\sim -\frac{E_0c\mathrm{e}^{\xi}}{2}\cos(\eta-\alpha)$

y esta, que ya es de por sí una solución de la ecuación de Laplace, nos dice cual es la solución del problema completo (que en 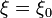$\xi = \xi_0\,$ tiene derivada nula). El potencial es

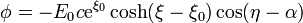
$\phi= -E_0c\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)\cos(\eta-\alpha)$

mientras que la función corriente, que nos da las líneas de campo, es

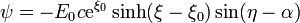
$\psi = -E_0c\mathrm{e}^{\xi_0}\sinh(\xi-\xi_0)\sin(\eta-\alpha)$

4 Momento dipolar

Para ver que esto equivale a un campo uniforme más un dipolo tenemos que demostrar que su comportamiento en puntos alejados va como

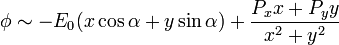
$\phi \sim -E_0(x\cos\alpha+y\sin\alpha) + \frac{P_xx+P_y y}{x^2+y^2}$

Para ello, en primer lugar, restamos el comportamiento asintótico

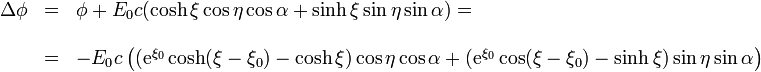
$\begin{array}{rcl}\Delta\phi & = & \phi + E_0 c(\cosh\xi\cos\eta\cos\alpha+\sinh\xi\sin\eta\sin\alpha)= \\ & & \\ & = & -E_0c\left((\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)-\cosh\xi)\cos\eta\cos\alpha+(\mathrm{e}^{\xi_0}\cos(\xi-\xi_0)-\sinh\xi)\sin\eta\sin\alpha\right)\end{array}$

Analizando los dos factores tenemos

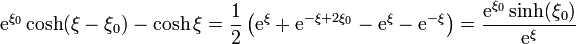
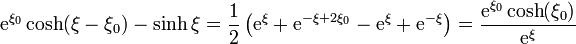
$\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)-\cosh\xi = \frac{1}{2}\left(\mathrm{e}^{\xi}+\mathrm{e}^{-\xi+2\xi_0}-\mathrm{e}^{\xi}-\mathrm{e}^{-\xi}\right) = \frac{\mathrm{e}^{\xi_0}\sinh(\xi_0)}{\mathrm{e}^{\xi}}$ $\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)-\sinh\xi = \frac{1}{2}\left(\mathrm{e}^{\xi}+\mathrm{e}^{-\xi+2\xi_0}-\mathrm{e}^{\xi}+\mathrm{e}^{-\xi}\right) = \frac{\mathrm{e}^{\xi_0}\cosh(\xi_0)}{\mathrm{e}^{\xi}}$

y por tanto

$\Delta\phi = -\frac{E_0c\mathrm{e}^{\xi_0}}{\mathrm{e}^\xi}\left(\sinh\xi_0\cos\eta\cos\alpha+\cosh\xi_0\sin\eta\sin\alpha\right)$

Para ver que esto es el potencial de una línea bifilar, observamos que para $ξ$ grande se cumple

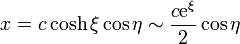
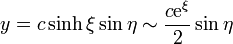
$x = c \cosh\xi\cos\eta \sim \frac{c\mathrm{e}^\xi}{2}\cos\eta$ $y = c \sinh\xi\sin\eta \sim \frac{c\mathrm{e}^\xi}{2}\sin\eta$

por lo que, en este mismo límite

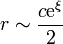
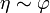
$r\sim \frac{c\mathrm{e}^\xi}{2}$ $\eta\sim\varphi$

lo que nos permite escribir el potencial residual en la forma asintótica

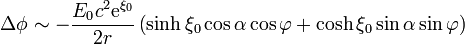
$\Delta\phi\sim -\frac{E_0c^2\mathrm{e}^{\xi_0}}{2r}\left(\sinh\xi_0\cos\alpha\cos\varphi+\cosh\xi_0\sin\alpha\sin\varphi\right)$

Podemos poner esta expresión en función de los datos originales observando que

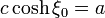
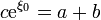
$c\cosh\xi_0=a\,$ $c\sinh\xi_0=b\,$ $c\mathrm{e}^{\xi_0}=a+b\,$

y queda

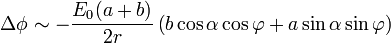
$\Delta\phi\sim -\frac{E_0(a+b)}{2r}\left(b\cos\alpha\cos\varphi+a\sin\alpha\sin\varphi\right)$

Comparando esto con el potencial de una línea bifilar de momento $\mathbf{P}$ por unidad de longitud

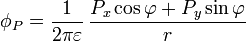
$\phi_P = \frac{1}{2\pi\varepsilon}\,\frac{P_x\cos\varphi+P_y\sin\varphi}{r}$

obtenemos que el momento dipolar visto desde el infinito es

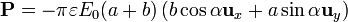
$\mathbf{P}=-\pi\varepsilon E_0(a+b)\left(b\cos\alpha\mathbf{u}_x+a\sin\alpha\mathbf{u}_y\right)$

5 Torque

Una vez que tenemos el momento dipolar y el campo aplicado, hallamos el par por unidad de longitud como

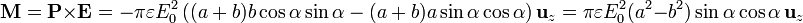
$\mathbf{M}=\mathbf{P}\times\mathbf{E}=-\pi\varepsilon E_0^2\left((a+b)b\cos\alpha\sin\alpha-(a+b)a\sin\alpha\cos\alpha\right)\mathbf{u}_z =\pi\varepsilon E_0^2(a^2-b^2)\sin\alpha\cos\alpha\,\mathbf{u}_z$

6 A partir del tensor de tensiones

El torque también debe poder calcularse a partir del flujo de 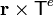$\mathbf{r}\times\mathsf{T}^e$ a través de una superficie que envuelva la partícula.

Considerando una superficie elíptica infinitamente próxima a la partícula se tiene que en ella

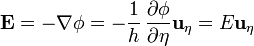
$\mathbf{E}=-\nabla\phi = -\frac{1}{h}\,\frac{\partial\phi}{\partial\eta}\mathbf{u}_\eta = E\mathbf{u}_\eta$

y el tensor de tensiones en esta superficie es

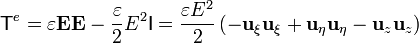
$\mathsf{T}^e=\varepsilon\mathbf{E}\mathbf{E}-\frac{\varepsilon}{2}E^2\mathsf{I}=\frac{\varepsilon E^2}{2}\left(-\mathbf{u}_\xi\mathbf{u}_\xi+\mathbf{u}_\eta\mathbf{u}_\eta-\mathbf{u}_z\mathbf{u}_{z}\right)$

El diferencial de superficie (por unidad de longitud vertical) es

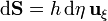
$\mathrm{d}\mathbf{S}=h\,\mathrm{d}\eta\,\mathbf{u}_\xi$

con lo que la contracción 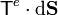$\mathsf{T}^e\cdot\mathrm{d}\mathbf{S}$ vale

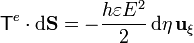
$\mathsf{T}^e\cdot\mathrm{d}\mathbf{S} = -\frac{h\varepsilon E^2}{2}\,\mathrm{d}\eta\,\mathbf{u}_\xi$

El vector de posición, en coordenadas elípticas, es

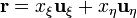
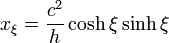
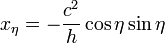
$\mathbf{r}=x_\xi\mathbf{u}_\xi+x_\eta\mathbf{u}_\eta\,$ $x_\xi=\frac{c^2}{h}\cosh\xi\sinh\xi$ $x_\eta =-\frac{c^2}{h}\cos\eta\sin\eta$

Multiplicando vectorialmente

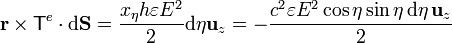
$\mathbf{r}\times\mathsf{T}^e\cdot\mathrm{d}\mathbf{S}=\frac{x_\eta h \varepsilon E^2}{2}\mathrm{d}\eta\mathbf{u}_z=-\frac{c^2\varepsilon E^2 \cos\eta\sin\eta\,\mathrm{d}\eta\,\mathbf{u}_z}{2}$

El valor de $E$ en la elipse es

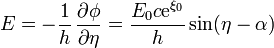
$E = -\frac{1}{h}\,\frac{\partial \phi}{\partial \eta} = \frac{E_0c\mathrm{e}^{\xi_0}}{h}\sin(\eta-\alpha)$

lo que nos da la integral para el momento

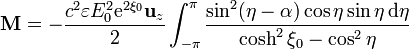
$\mathbf{M}=-\frac{c^2\varepsilon E_0^2\mathrm{e}^{2\xi_0}\mathbf{u}_z}{2}\int_{-\pi}^\pi \frac{\sin^2(\eta-\alpha)\cos\eta\sin\eta\,\mathrm{d}\eta}{\cosh^2\xi_0-\cos^2\eta}$

Desarrollando $sin 2 (η - α)$

$\sin^2(\eta-\alpha) = \sin^2\eta\cos^2\alpha+\cos^2\eta\sin^2\alpha-2\sin\eta\cos\eta\sin\alpha\cos\alpha\,$

Los dos primeros términos, al integrarlos, dan cero, por tratarse de un integrando impar sobre un intervalo par. Queda entonces

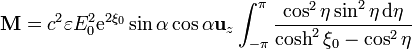
$\mathbf{M}=c^2\varepsilon E_0^2\mathrm{e}^{2\xi_0}\sin\alpha\cos\alpha\mathbf{u}_z\int_{-\pi}^\pi \frac{\cos^2\eta\sin^2\eta\,\mathrm{d}\eta}{\cosh^2\xi_0-\cos^2\eta}$

Esta integral se puede hacer, por ejemplo, por residuos (o usando el Mathematica), y sale

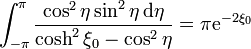
$\int_{-\pi}^\pi \frac{\cos^2\eta\sin^2\eta\,\mathrm{d}\eta}{\cosh^2\xi_0-\cos^2\eta} =\pi \mathrm{e}^{-2\xi_0}$

así que obtenemos finalmente

$\mathbf{M}=\pi \varepsilon E_0^2(a^2-b^2)\sin\alpha\cos\alpha\mathbf{u}_z$

Partícula elíptica en campo eléctrico oblicuo

De Laplace

Contenido

1 Planteamiento

2 Coordenadas elípticas

3 Solución para el potencial

4 Momento dipolar

5 Torque

6 A partir del tensor de tensiones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES