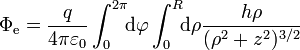Flujo del campo eléctrico de una carga
De Laplace
Contenido |
1 Enunciado
Halle el flujo del campo eléctrico debido a una carga puntual q a través de un disco cuyo eje pasa por el punto donde se encuentra la carga.
El disco tiene radio R y la distancia de la carga al plano del disco es h.
- Utilizando coordenadas cilíndricas
- Usando coordenadas esféricas (Sugerencia: En lugar del disco emplee otra superficie que abarque el mismo ángulo sólido).
2 Introducción
El flujo del campo eléctrico de una carga puntual (sobre la cual, por comodidad, situamos el origen de coordenadas) es
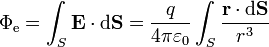
La integral que aparece en el último miembro no es más que el ángulo sólido, Ω, abarcado por la superficie, vista desde el origen de coordenadas. Por tanto
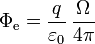
El problema se reduce, por tanto, a determinar el ángulo sólido con el que el disco se ve desde la carga.
3 En cilíndricas
Sitaumos, según hemos dicho, el origen de coordenadas sobre la carga puntual, y el eje Z como el eje del disco. De esta forma, el disco queda parametrizado como
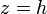
![\rho\in[0,R]](/wiki/images/math/5/a/2/5a2c43a0583cd93d6b8f87dc84b97962.png)
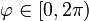
El vector de posición de los puntos del disco y el vector diferencial de superficie valen
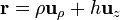
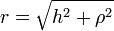
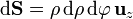 {
{ 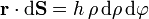
Sustituimos en la expresión del flujo