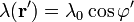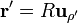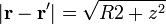Entrar Página Discusión Historial Go to the site toolbox

Campo de un anillo no uniforme

De Laplace

Contenido

1 Enunciado

En el plano XY se encuentra una distribución de carga lineal, formando un anillo, de radio R y con una distribución de carga no uniforme dada, en coordenadas cilíndricas, por

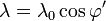
\lambda=\lambda_0\cos\varphi'    \varphi'\in(-\pi,\pi]
  1. Halle el potencial eléctrico producido por el anillo en los puntos del eje Z.
  2. Calcule el campo eléctrico producido por el anillo en el mismo eje.
  3. Demuestre que, para puntos alejados, su campo se comporta como el de un dipolo, ¿cuál sería el valor y la orientación de dicho dipolo?

2 Potencial en el eje

El potencial en el eje del anillo puede hallarse por integración directa, según la expresión

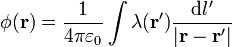
\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}

Tenemos que

\lambda(\mathbf{r}')=\lambda_0\cos\varphi'        \mathbf{r}=z\mathbf{u}_z\,        \mathbf{r}'=R\mathbf{u}_{\rho'}\,        \mathbf{r}-\mathbf{r}'=-R\mathbf{u}_{\rho'}+z\mathbf{u}_z\,        |\mathbf{r}-\mathbf{r}'|=\sqrt{R2+z^2}        \mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'

3 Campo en el eje

4 Desarrollo multipolar

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_de_un_anillo_no_uniforme"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace