Entropía
De Laplace
Contenido |
1 Introducción
2 Desigualdad de Clausius
3 Definición de entropía
Para un ciclo reversible, la desigualdad se transforma en una igualdad. Si tomamos un ciclo que vaya de un estado 1 a un estado 2, por un cierto camino reversible C, o volvemos por otro también reversible C', la igualdad se convierte en
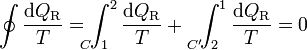
Por ser los caminos reversibles, la integral de 2 a 1 por C' es igual a la integral de 1 a 2 por el mismo camino C', cambiada de signo. Esto implica
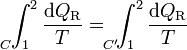
Puesto que esto es cierto para cualquier otro camino reversible que conecte 1 con 2, concluimos que el valor de la integral es independiente del camino y por tanto solo depende de los estados inicial y final. Por tanto, su valor es igual a la diferencia de una cierta función de estado que denominamos entropía
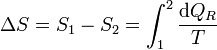
o, en forma diferencial
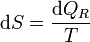
Obsérvese que esta definición sólo nos da el incremento de entropía entre dos estados, no el valor absoluto en cada uno de ellos. Por ello, es preciso definir un estado de referencia a partir del cual se mide la entropía.





