Variación de entropía con un baño térmico
De Laplace
Contenido |
1 Enunciado
Un tanque de volumen constante contiene 100 moles de aire a una presión de 100 kPa y una temperatura de 327°C. El aire se enfría hasta la temperatura del ambiente de 27.0°C. Suponiendo que el aire se comporta como un gas ideal diatómico, determine la variación de entropía del aire y del Universo durante el proceso.
2 Variación de entropía del ambiente
Cuando el aire se enfría intercambia una cierta cantidad de calor igual a
Puesto que el proceso ocurre a volumen constante, el trabajo realizado sobre el gas es nulo y el calor equivale a la variación de la energía interna
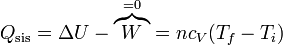
cuyo valor es
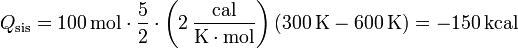
Este calor es negativo pues en realidad sale del sistema
El calor que entra en el ambiente es este mismo, cambiado de signo
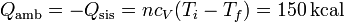
Esta entrada de calor se produce a una temperatura constante (en el ambiente), por lo que el aumento de entropía del ambiente es






