Entropía de una mezcla de gases

De Laplace

Revisión a fecha de 18:32 28 abr 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Entropía de un gas ideal
3 Entropía de una mezcla
4 Incremento de entropía

1 Enunciado

Un recipiente de 2.00 l tiene una barrera que lo divide por la mitad. Una mitad contiene H₂ y la otra O₂. Ambos gases se encuentran a temperatura ambiente y presión atmosférica. Se retira la barrera de separación, permitiendo que los gases se mezclen. ¿Cuál el aumento de entropía del sistema?

2 Entropía de un gas ideal

2.1 Expresión en función de T y V

Para un gas ideal puro, podemos calcular el incremento diferencial de entropía a partir de la definición

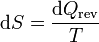
$\mathrm{d}S=\frac{\mathrm{d}Q_\mathrm{rev}}{T}$

A su vez, el diferencial de calor reversible puede hallarse mediante el primer principio de la termodinámica

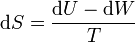
$\mathrm{d}S=\frac{\mathrm{d}U-\mathrm{d}W}{T}$

Para un gas ideal sabemos que

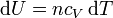
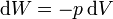
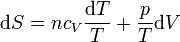
$\mathrm{d}U = nc_V\,\mathrm{d}T$ $\mathrm{d}W=-p\,\mathrm{d}V$ $\Rightarrow$ $\mathrm{d}S=nc_V\frac{\mathrm{d}T}{T}+\frac{p}{T}\mathrm{d}V$

Sustituyendo la ecuación de estado del gas ideal

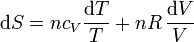
$\mathrm{d}S = nc_V\frac{\mathrm{d}T}{T}+nR\,\frac{\mathrm{d}V}{V}$

Si suponemos que la capacidad calorífica molar es independiente de la temperatura, podemos integrar esta ecuación para hallar el incremento entre dos estados

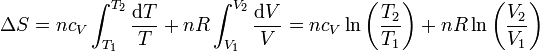
$\Delta S = nc_V\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}+nR\int_{V_1}^{V_2}\frac{\mathrm{d}V}{V}= nc_V\ln\left(\frac{T_2}{T_1}\right)+nR\ln\left(\frac{V_2}{V_1}\right)$

2.2 Expresión en función de T y p

Si lo que tenemos es el cambio en la presión, en lugar del volumen, podemos hacer un cálculo análogo empleando la entalpía

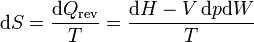
$\mathrm{d}S=\frac{\mathrm{d}Q_\mathrm{rev}}{T}=\frac{\mathrm{d}H-V\,\mathrm{d}p\mathrm{d}W}{T}$

La entalpía se relaciona con la temperatura a través de la capacidad calorífica a presión constante

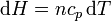
$\mathrm{d}H = nc_p\,\mathrm{d}T$

lo que lleva a la expresión para el incremento de entropía

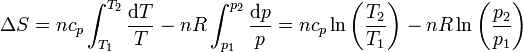
$\Delta S = nc_p\int_{T_1}^{T_2}\frac{\mathrm{d}T}{T}-nR\int_{p_1}^{p_2}\frac{\mathrm{d}p}{p}= nc_p\ln\left(\frac{T_2}{T_1}\right)-nR\ln\left(\frac{p_2}{p_1}\right)$

También se puede llegar a este resultado sustituyendo la ecuación de los gases ideales en la expresión en función de T y V.

2.3 Expansión adiabática

Si tenemos un conjunto de moles de un gas que se expande de un volumen V a un volumen 2V, siendo la temperatura final la misma que la inicial, la variación en la entropía del gas es

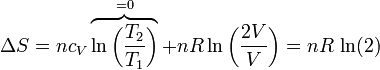
$\Delta S = nc_V\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}+nR\ln\left(\frac{2V}{V}\right) = nR\,\ln(2)$

Si usamos como variables la temperatura y la presión (que tienen la ventaja de ser ambas variables intensivas), lo que vemos es que la presión se reduce a la mitad

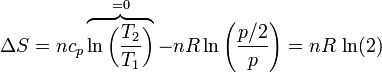
$\Delta S = nc_p\overbrace{\ln\left(\frac{T_2}{T_1}\right)}^{=0}-nR\ln\left(\frac{p/2}{p}\right) = nR\,\ln(2)$

que naturalmente coincide con el resultado anterior.

3 Entropía de una mezcla

4 Incremento de entropía

Entropía de una mezcla de gases

De Laplace

Contenido

1 Enunciado

2 Entropía de un gas ideal

2.1 Expresión en función de T y V

2.2 Expresión en función de T y p

2.3 Expansión adiabática

3 Entropía de una mezcla

4 Incremento de entropía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES