Entrar Página Discusión Historial Go to the site toolbox

Campo de un solenoide cilíndrico

De Laplace

Contenido

1 Enunciado

Un solenoide de radio a, altura h y n espiras por unidad de longitud, puede aproximarse por una distribución de corriente superficial sobre un cilindro.

  1. Halle el valor 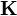\mathbf{K} equivalente a que por las espiras circule una corriente I.
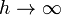  2. Empleando las leyes de la magnetostática, calcule el campo producido por el solenoide, si h\to\infty.
  3. Mediante integración directa, halle el campo magnético en los puntos del eje del cilindro si h es finito. Estudie el límite h \gg a

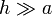
2 Densidad superficial de corriente

Dada una densidad de corriente superficial, la relación entre ésta y la intensidad de corriente total que atraviesa una línea trazada en la superficie es

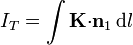
I_T=\int \mathbf{K}{\cdot}\mathbf{n}_1\,\mathrm{d}l

donde 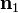\mathbf{n}_1 es un vector unitario normal a la curva y tangente a la superficie.

Para establecer la correspondencia entre la corriente que circula por el solenoide y la densidad de corriente equivalente, imponemos que sea idéntica la corriente total que atraviesa una línea vertical trazada sobre el solenoide. Esta línea corta $N$ espiras, siendo

N=nh\,

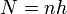
por lo que la corriente total que atraviesa la línea es

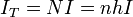
I_T=NI=nhI\,

con I la intensidad que circula por cada espira. Si se supone una densidad de corriente superficial 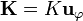\mathbf{K}=K\mathbf{u}_{\varphi} resulta

I_T=\int_0^h(K\mathbf{u}_{\varphi}){\cdot}\mathbf{u}_{\varphi}\,\mathrm{d}z=Kh

Igualando ambas cantidades se tiene la relación

K=nI\,

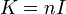
o, equivalentemente K = NI / h.

3 Campo en un solenoide infinito

4 Campo en un solenoide finito

El campo en los puntos del eje puede aproximarse a partir de la superposición del campo de N espiras, situada cada una a una altura zi. El campo debido a cada una de estas espiras va en la dirección del eje Z y depende de la altura como una función en forma de campana.

\mathbf{B}\simeq\sum_{i=1}^N \frac{\mu_0I R^2 \mathbf{u}_z}{2(R^2+(z-z_i)^2)^{3/2}}

Esta expresión es aproximada porque sustituye lo que en realidad es una hélice por un conjunto de espiras circulares desconectadas entre sí.

La distancia Δz' entre dos espiras sucesivas es aproximadamente la inversa de la densidad (cuando N es grande), ya que

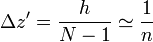
\Delta z' = \frac{h}{N-1}\simeq\frac{1}{n}

En el caso de un solenoide densamente arrollado esta distancia equivale al diámetro del hilo, ya que no quedan intersticios entre vueltas sucesivas.

Esto nos permite expresar el sumatorio como

\mathbf{B}=\sum_{i=1}^N \frac{\mu_0nI R^2 \Delta z'\mathbf{u}_z}{2(R^2+(z-z_i)^2)^{3/2}}

pero nI = K es la densidad de corriente superficial equivalente. Por otra parte, podemos escribir el sumatorio en términos de z' = zi, en vez de i, lo que nos deja el sumatorio como

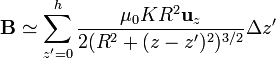
\mathbf{B}\simeq\sum_{z'=0}^h \frac{\mu_0K R^2\mathbf{u}_z}{2(R^2+(z-z')^2)^{3/2}} \Delta z'

y, teniendo en cuenta que Δz' es una cantidad muy pequeña, comparada con la longitud de la bobina, podemos aproximar el sumatorio por una integral

\mathbf{B}\simeq\int_0^h \frac{\mu_0K R^2\mathbf{u}_z}{2(R^2+(z-z')^2)^{3/2}} \mathrm{d}z'

Para resolver esta integral, como en el problema del campo magnético de un segmento, hacemos el cambio de variable

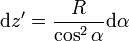
z'-z=R\,\mathrm{tg}\,\alpha         R^2+(z-z')^2=\frac{R^2}{\cos^2\alpha}        \mathrm{d}z'=\frac{R}{\cos^2\alpha}\mathrm{d}\alpha

En este caso, α representa la elevación con la que se ve un punto del solenoide, visto desde un punto del eje. Este cambio de variable transforma la integral en

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathbf{B}=\frac{\mu_0K\mathbf{u}_z}{2}\int_{\alpha_1}^{\alpha}_2\!\!\cos\alpha \mathrm{d}\alpha=\frac{\mu_0K\mathbf{u}_z}{2}\left(\,\mathrm{sen}\alpha_2-\,\mathrm{sen}\,\alpha_1)

con α1 y α2

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_de_un_solenoide_cil%C3%ADndrico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace