Acción de un campo magnético sobre un dipolo magnético

De Laplace

1 Introducción

Un dipolo magnético, tanto si es una corriente localizada como si posee un momento intrínseco, experimenta la acción de un campo magnético externo, que tiende a moverlo y orientarlo.

Este efecto es análogo al caso de un dipolo eléctrico en el seno de un campo eléctrico. El dipolo experimenta una fuerza y un momento de una fuerza, y posee una cierta energía potencial

Es posible deducir las expresiones de la fuerza y el par sobre el dipolo a partir de la fuerza de Lorentz para una distribución de corriente.

2 Fuerza

La fuerza experimentada por un dipolo magnético en un campo externo es

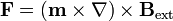
que, para el caso de un dipolo de momento constante, puede transformarse en la expresión más manejable

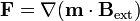
Esta transformación no es aplicable en el caso de dipolos inducidos (aquellos, que como en el caso de una partícula magnética en un campo externo) para los cuales el momento dipolar depende del campo externo aplicado y por tanto es función de la posición.

Si además el dipolo no se encuentra sumergido en una distribución de corriente, la fuerza se puede transformar en

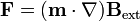
que es la análoga de la fuerza eléctrica sobre un dipolo eléctrico

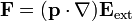
2.1 Demostración

Partimos de la fuerza de Lorentz sobre una corriente lineal

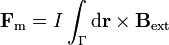
Si aplicamos la generalización del teorema de Stokes a esta integral la transformamos en

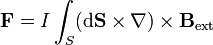
siendo S una superficie apoyada en la curva Γ. Si podemos usar la aproximación de la espira como un dipolo magnético esta superficie es muy pequeña, de forma que podemos suponer que el campo magnético y su gradiente tienen el mismo valor en todos los puntos de la espira. Con esta aproximación, la fuerza se convierte en

Esta es la primera expresión para la fuerza.

Ahora bien, si 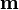es un vector constante la expresión anterior es equivalente a

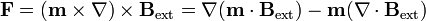
sin más que aplicar la fórmula del doble producto vectorial. Puesto que el campo magnético es solenoidal el segundo término se anula y la fuerza se reduce a

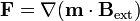
Esta segunda expresión es la más fácil de calcular. No obstante, no es completamente análoga a la fuerza eléctrica sobre un dipolo eléctrico, ya que en el caso eléctrico el momento dipolar está fuera de la derivada (en ese sentido, la primera expresión sería más parecida, cambiando los productos escalares por vectoriales). Podemos conseguir una expresión completamente análoga desarrollando el gradiente de un producto escalar

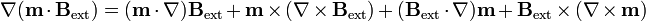
Si el momento dipolar es constante, los dos últimos términos se anulan. El segundo término, de acuerdo con la ley de Ampère equivale a

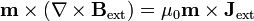
siendo 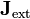la densidad de corriente que crea el campo aplicado 8no la que forma el propio dipolo). En muchos casos el dipolo no se encuentra sumergido en la propia corriente, sino en una región vacía, experimentando un campo aplicado desde fuera (por ejemplo, entre los polos de un imán). En ese caso esta densidad de corriente se anula en la posición del dipolo, 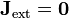y la fuerza se reduce a

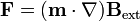
que si es análoga a la fuerza eléctrica sobre un dipolo eléctrico.

Obsérvese que para transformar la segunda forma en la tercera no se ha aplicado propiedad asociativa o conmutativa que valga; para empezar porque el producto escalar no es asociativo, es más, ni siquiera existe el producto escalar de tres vectores

3 Par y momento

El momento sobre el dipolo se compone del momento de la fuerza aplicada, más un término intrínseco:

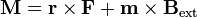
El segundo término representa un par intrínseco que tiende a alinear el dipolo con el campo magnético, lo que constituye el fundamento de las brújulas.

3.1 El caso de un campo uniforme

Supongamos una espira cerrada en el seno de un campo magnético uniforme. La fuerza diferencial sobre un elemento de corriente de la espira es

y el momento de esta fuerza diferencial

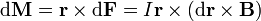
y el momento total de las fuerzas aplicadas sobre la espira es

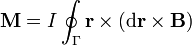
4 Energía

Tanto la fuerza como el momento pueden derivarse de la energía de un dipolo en un campo externo

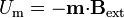
Esta energía es mínima cuando el dipolo apunta en la misma dirección y sentido que el campo aplicado sobre él.