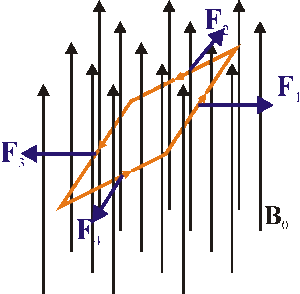
Acción de un campo magnético sobre un dipolo magnético

De Laplace

Contenido

1 Introducción
2 Fuerza
- 2.1 Demostración
3 Par y momento
- 3.1 Espira rectangular en un campo uniforme
- 3.2 Dipolo en un campo no uniforme
4 Energía

1 Introducción

Un dipolo magnético, tanto si es una corriente localizada como si posee un momento intrínseco, experimenta la acción de un campo magnético externo, que tiende a moverlo y orientarlo.

Este efecto es análogo al caso de un dipolo eléctrico en el seno de un campo eléctrico. El dipolo experimenta una fuerza y un momento de una fuerza, y posee una cierta energía potencial

Es posible deducir las expresiones de la fuerza y el par sobre el dipolo a partir de la fuerza de Lorentz para una distribución de corriente.

2 Fuerza

La fuerza experimentada por un dipolo magnético en un campo externo es

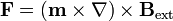
$\mathbf{F}= (\mathbf{m}\times\nabla)\times\mathbf{B}_\mathrm{ext}$

que, para el caso de un dipolo de momento constante, puede transformarse en la expresión más manejable

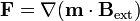
$\mathbf{F}= \nabla(\mathbf{m}\cdot\mathbf{B}_\mathrm{ext})$

Esta transformación no es aplicable en el caso de dipolos inducidos (aquellos, que como en el caso de una partícula magnética en un campo externo) para los cuales el momento dipolar depende del campo externo aplicado y por tanto es función de la posición.

Si además el dipolo no se encuentra sumergido en una distribución de corriente, la fuerza se puede transformar en

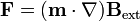
$\mathbf{F}= (\mathbf{m}\cdot\nabla)\mathbf{B}_\mathrm{ext}$

que es la análoga de la fuerza eléctrica sobre un dipolo eléctrico

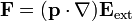
$\mathbf{F}= (\mathbf{p}\cdot\nabla)\mathbf{E}_\mathrm{ext}$

2.1 Demostración

Partimos de la fuerza de Lorentz sobre una corriente lineal

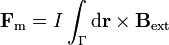
$\mathbf{F}_\mathrm{m}=I\int_\Gamma \mathrm{d}\mathbf{r}\times\mathbf{B}_\mathrm{ext}$

Si aplicamos la generalización del teorema de Stokes a esta integral la transformamos en

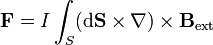
$\mathbf{F}= I\int_S (\mathrm{d}\mathbf{S}\times\nabla)\times\mathbf{B}_\mathrm{ext}$

siendo $S$ una superficie apoyada en la curva $Γ$ . Si podemos usar la aproximación de la espira como un dipolo magnético esta superficie es muy pequeña, de forma que podemos suponer que el campo magnético y su gradiente tienen el mismo valor en todos los puntos de la espira. Con esta aproximación, la fuerza se convierte en

$\mathbf{F}= I(\mathbf{S}\times\nabla)\times\mathbf{B}_\mathrm{ext}= (\mathbf{m}\times\nabla)\times\mathbf{B}_\mathrm{ext}$

Esta es la primera expresión para la fuerza.

Ahora bien, si 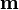$\mathbf{m}$ es un vector constante la expresión anterior es equivalente a

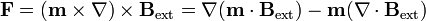
$\mathbf{F}= (\mathbf{m}\times\nabla)\times\mathbf{B}_\mathrm{ext}=\nabla(\mathbf{m}\cdot\mathbf{B}_\mathrm{ext})-\mathbf{m}(\nabla\cdot\mathbf{B}_\mathrm{ext})$

sin más que aplicar la fórmula del doble producto vectorial. Puesto que el campo magnético es solenoidal el segundo término se anula y la fuerza se reduce a

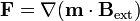
$\mathbf{F}=\nabla(\mathbf{m}\cdot\mathbf{B}_\mathrm{ext})$

Esta segunda expresión es la más fácil de calcular. No obstante, no es completamente análoga a la fuerza eléctrica sobre un dipolo eléctrico, ya que en el caso eléctrico el momento dipolar está fuera de la derivada (en ese sentido, la primera expresión sería más parecida, cambiando los productos escalares por vectoriales). Podemos conseguir una expresión completamente análoga desarrollando el gradiente de un producto escalar

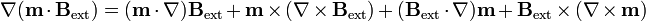
$\nabla(\mathbf{m}\cdot\mathbf{B}_\mathrm{ext}) = (\mathbf{m}\cdot\nabla)\mathbf{B}_\mathrm{ext}+\mathbf{m}\times(\nabla\times\mathbf{B}_\mathrm{ext})+(\mathbf{B}_\mathrm{ext}\cdot\nabla)\mathbf{m}+\mathbf{B}_\mathrm{ext}\times(\nabla\times\mathbf{m})$

Si el momento dipolar es constante, los dos últimos términos se anulan. El segundo término, de acuerdo con la ley de Ampère equivale a

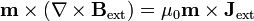
$\mathbf{m}\times(\nabla\times\mathbf{B}_\mathrm{ext}) = \mu_0\mathbf{m}\times\mathbf{J}_\mathrm{ext}$

siendo 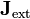$\mathbf{J}_\mathrm{ext}$ la densidad de corriente que crea el campo aplicado 8no la que forma el propio dipolo). En muchos casos el dipolo no se encuentra sumergido en la propia corriente, sino en una región vacía, experimentando un campo aplicado desde fuera (por ejemplo, entre los polos de un imán). En ese caso esta densidad de corriente se anula en la posición del dipolo, 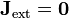$\mathbf{J}_\mathrm{ext}=\mathbf{0}$ y la fuerza se reduce a

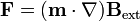
$\mathbf{F}=(\mathbf{m}\cdot\nabla)\mathbf{B}_\mathrm{ext}$

que si es análoga a la fuerza eléctrica sobre un dipolo eléctrico.

Obsérvese que para transformar la segunda forma en la tercera no se ha aplicado propiedad asociativa o conmutativa que valga; para empezar porque el producto escalar no es asociativo, es más, ni siquiera existe el producto escalar de tres vectores

3 Par y momento

El momento sobre el dipolo se compone del momento de la fuerza aplicada, más un término intrínseco:

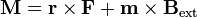
$\mathbf{M}=\mathbf{r}\times\mathbf{F} + \mathbf{m}\times\mathbf{B}_\mathrm{ext}$

El segundo término representa un par intrínseco que tiende a alinear el dipolo con el campo magnético, lo que constituye el fundamento de las brújulas.

3.1 Espira rectangular en un campo uniforme

En lugar de demostrar rigurosamente el resultado anterior, que requiere una cantidad considerable de cálculo vectorial, nos limitaremos a inducirlo e interpretarlo.

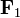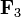Una espira en un campo uniforme experimenta una fuerza nula, pero ello no implica que no se mueva por efecto del campo. Al aplicarse en diferentes partes del circuito, el campo produce un momento (un par de fuerzas) que genera rotación. En la figura, el par lo forman las fuerzas $\mathbf{F}_1$ y $\mathbf{F}_3$ .

Supongamos que la espira posee lado $a$ , está recorrida por una corriente $I$ y el vector normal al plano de la espira forma un ángulo $θ$ con el campo magnético.

En lugar de una integral podemos usar el sumatorio, considerando la fuerza sobre cada segmento de la espira

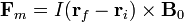
$\mathbf{F}_m=I(\mathbf{r}_f-\mathbf{r}_i)\times\mathbf{B}_0$

Si tomamos como eje Z el señalado por el campo magnético y como eje Y el de las varillas horizontales, las cuatro fuerzas valen

Sobre el lado superior

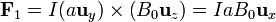
$\mathbf{F}_1=I(a\mathbf{u}_y)\times\left(B_0\mathbf{u}_z\right)=IaB_0\mathbf{u}_x$

Sobre el lado del fondo

$\mathbf{F}_2=I(a(-\cos\theta\mathbf{u}_x-a\,\mathrm{sen}\,\theta\mathbf{u}_z)\times\left(B_0\mathbf{u}_z\right)=IaB_0\cos\theta\mathbf{u}_y$

3.2 Dipolo en un campo no uniforme

Si el campo magnético varía con la posición, pero su variación es suave, podemos suponer que el campo magnético tiene el mismo valor en todos los puntos de la espira, con lo que el par sobre ella sigue siendo el mismo, 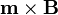$\mathbf{m}\times\mathbf{B}$ . Sin embargo, en este caso, la fuerza sobre el dipolo no es nula, según vimos en el apartado anterior. Por ello, el momento total de las fuerzas incluye la contribución del momento de la fuerza neta, más el momento intrínseco

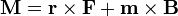
$\mathbf{M}=\mathbf{r}\times\mathbf{F}+\mathbf{m}\times\mathbf{B}$

El efecto del segundo término, según hemos dicho, consiste en alinear el dipolo con el campo aplicado. El primero produce una rotación en torno al origen de coordenadas. Si no hay fuerza neta, o el origen de coordenadas se encuentra en el propio dipolo, este término es nulo.

Sobre el lado inferior

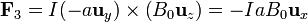
$\mathbf{F}_3=I(-a\mathbf{u}_y)\times\left(B_0\mathbf{u}_z\right)=-IaB_0\mathbf{u}_x$

Sobre el lado del frente

$\mathbf{F}_4=I(a(\cos\theta\mathbf{u}_x+a\,\mathrm{sen}\,\theta\mathbf{u}_z)\times\left(B_0\mathbf{u}_z\right)=-IaB_0\cos\theta\mathbf{u}_y$

La resultante de las fuerzas es naturalmente nula

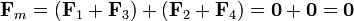
$\mathbf{F}_m=(\mathbf{F}_1+\mathbf{F}_3)+(\mathbf{F}_2+\mathbf{F}_4)=\mathbf{0}+\mathbf{0}=\mathbf{0}$

El momento de las fuerzas 2 y 4 se anula también ya que vector de posición del punto de aplicación de cada una (el centro de la varilla) es paralelo a la fuerza en ese segmento

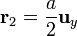
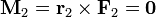
$\mathbf{r}_2=\frac{a}{2}\mathbf{u}_y$ $\Rightarrow$ $\mathbf{M}_2=\mathbf{r}_2\times\mathbf{F}_2=\mathbf{0}$

Para los lados 1 y 3, teniendo en cuenta que las fuerzas en ellos son iguales y opuestas

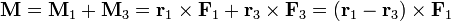
$\mathbf{M}=\mathbf{M}_1+\mathbf{M}_3=\mathbf{r}_1\times\mathbf{F}_1+\mathbf{r}_3\times\mathbf{F}_3=(\mathbf{r}_1-\mathbf{r}_3)\times\mathbf{F}_1$

Sustituyendo las posiciones

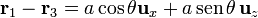
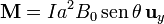
$\mathbf{r}_1-\mathbf{r}_3=a\cos\theta\mathbf{u}_x+a\,\mathrm{sen}\,\theta\,\mathbf{u}_z$ $\Rightarrow$ $\mathbf{M}=Ia^2B_0\,\mathrm{sen}\,\theta\,\mathbf{u}_y$

Si introducimos el vector momento magnético de la espira

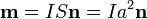
$\mathbf{m}=IS\mathbf{n}=Ia^2\mathbf{n}$

este momento de la fuerza lo podemos escribir

$\mathbf{M} = \mathbf{m}\times\mathbf{B}$

La dirección y el sentido del momento de la fuerza (en el de $+\mathbf{u}_y$ , en este ejemplo), indica el eje y el sentido de giro que tiende a efectuar la espira. La espira intenta orientarse de forma que su vector momento magnético quede alineado con el campo aplicado.

El momento sobre una espira de corriente es la base de los amperímetros analógicos: Se hace pasar la corriente que se quiere medir por el interior de un campo. La medida del par que produce $\mathbf{B}$ permite conocer la corriente.

4 Energía

De la segunda expresión para la fuerza podemos escribir ésta como el gradiente de una energía potencial

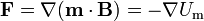
$\mathbf{F}=\nabla(\mathbf{m}\cdot\mathbf{B})=-\nabla U_\mathrm{m}$

siendo la energía potencial

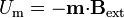
$U_\mathrm{m}=-\mathbf{m}{\cdot}\mathbf{B}_\mathrm{ext}$

A partir de esta energía puede también derivarse el momento de la fuerza debido al campo externo.

Esta energía es mínima cuando el dipolo apunta en la misma dirección y sentido que el campo aplicado sobre él. Para ver por qué, basta con expresar el producto de los módulos por el coseno del ángulo que formanº

$U_m = -|\mathbf{m}||\mathbf{B}_\mathrm{ext}|\cos\alpha$

En un punto dado, ambos módulos tienen un valor fijado, por lo que el mínimo valor de la energía se alcanza cuando el coseno vale +1, esto es, cuando ambos vectores tienen la misma dirección y sentido.

Acción de un campo magnético sobre un dipolo magnético

De Laplace

Contenido

1 Introducción

2 Fuerza

2.1 Demostración

3 Par y momento

3.1 Espira rectangular en un campo uniforme

3.2 Dipolo en un campo no uniforme

4 Energía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES