Campo magnético de una espira rectangular
De Laplace
Revisión a fecha de 17:25 25 mar 2009; Antonio (Discusión | contribuciones)
1 Enunciado
Calcule el campo magnético en el centro de una espira rectangular de lados a y b, por la cual circula una corriente continua I.
¿A qué se reducen los resultados si a = b? ¿Y si 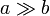 ?
?
2 Solución
El campo debido a un segmento rectilíneo puede escribirse en la forma
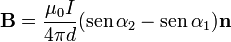
siendo α1 y α2 los ángulos con los que se ven los extremos del segmento desde el punto donde queremos hallar el campo, y \mathbf{n} es la normal al plano definido por el segmento





