Potencial vector magnético

De Laplace

De que el campo magnético sea solenoidal se deduce que puede escribirse como el rotacional de otro campo vectorial, denominado potencial vector magnético

      

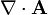
de hecho, al demostrar la ley de Gauss para el campo magnético ya se da una expresión para este potencial vector

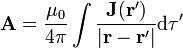
sin embargo, esta expresión, aparte de que sólo vale para corrientes estacionarias, no es la única posible. Dado un campo magnético, existen infinitos potenciales vectores posibles, los cuales se diferencian en el gradiente de una función escalar arbitraria

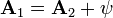
siendo la demostración inmediata, sin más que tomar el rotacional de ambos miembros. La libertad de elección de ψ hace que podamos tener potenciales vectores muy diferentes para el mismo campo.

La utilidad del potencial vector es limitada, por su naturaleza vectorial, que hace que no reduzca sustancialmente el problema del cálculo de \mathbf{B}.

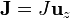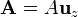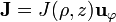Sirve como herramienta en los casos en que tenemos corrientes fluyendo siempre según la misma componente. Por ejemplo, si podemos suponer . Si podemos suponer 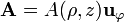. En estos casos el cálculo del potencial vector se reduce a determinar una sola componente, de forma similar a como se hace con el potencial escalar del campo electrostático. La otra utilidad del potencial vector es su uso en deducciones teóricas acerca del campo magnético y para el electromagnético, Uno de estos casos es en el desarrollo multipolar magnético.