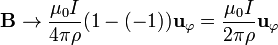Campo magnético de una corriente rectilínea
De Laplace
Contenido |
1 Enunciado
Halle, por integración directa, el campo magnético producido en todo el espacio por un segmento rectilíneo de longitud L por el cual circula una corriente continua I.
A partir del resultado anterior, halle el campo producido en todos los puntos del espacio por un hilo de longitud infinita por el cual circula una corriente continua I.
Para el caso de un hilo infinito, determine este mismo campo magnético partiendo de las ecuaciones de la magnetostática.
2 Por integración directa
2.1 Segmento finito
Una varilla aislada de longitud finita no puede encontrarse en un estado estacionario, ya que la carga que circulara por ella al llegar al extremo no podría desvanecerse, sino que produciría una acumulación progresiva de carga, que ya no sería estacionaria. Sin embargo, si el segmento forma parte de una curva cerrada, como un polígono, podemos aplicar el principio de superposición a cada uno de sus lados, calculados como si se trataran de segmentos aislados.
El campo debido a una sola varilla de corriente de longitud L lo podemos calcular suponiendo el eje Z sobre la varilla, y que ésta se extiende desde − L / 2 hasta L / 2, fluyendo la corriente hacia valores de z crecientes. Según la ley de Biot y Savart, el campo magnético en un punto cualquiera del espacio es
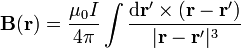
En este caso
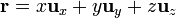
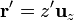
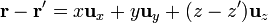
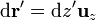
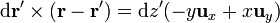
y el cálculo del campo se reduce a la integral
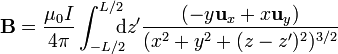
Esta integral se resuelve con el cambio de variable
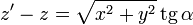
donde α es el ángulo que forma con la perpendicular al segmento el vector 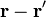 . El resultado final es
. El resultado final es
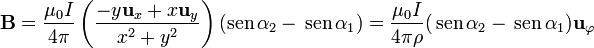
Según esto, el campo debido a la varilla va en la dirección acimutal en torno a la varilla y su valor depende de la distancia $\rho$ al eje de la varilla, y de los ángulos con que se ven los extremos.
2.2 Violación de la ley de Ampére
Podemos comprobar que el campo debido a un único segmento no verifica la ley de Ampère, la cual solo es cierta para corrientes estacionarias, entre las cuales no se cuenta este sistema, según hemos dicho. Para ello calculamos la circulación a través de una curva cerrada alrededor del segmento
Tomando una curva circular, de radio ρ, concéntrica con el eje Z, a una altura z0 sobre el plano XY, resulta
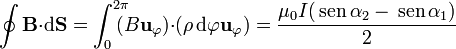
De acuerdo con la ley de Ampère esta circulación debería ser igual o μ0I o 0 si el disco apoyado en la circunferencia corta al segmento o no lo hace. El resultado real no es ninguno de estos dos.
2.3 Hilo infinito
Como caso particular de esta expresión tenemos el caso de un hilo infinito, pero de radio nulo. Para 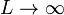 , se verifica
, se verifica
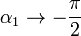
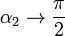
y el límite del campo es