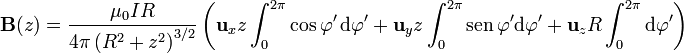Campo magnético debido a una corriente

De Laplace

Revisión a fecha de 17:46 19 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Campo producido por una carga en movimiento
- 2.1 El magnetismo y la 3ª ley de Newton
- 2.2 Fuerza entre dos cargas en movimiento paralelo
3 Campo creado por una distribución de corriente

1 Introducción

Al estudiar la ley de Lorentz se describe la acción que un campo magnético produce sobre una carga en movimiento o un conjunto de ellas. La siguiente cuestión es quién produce dicho campo magnético.

De acuerdo con la simetría establecida por Ampère, del mismo modo que las cargas en movimiento experimentan el campo magnético, también son su causa.

La corrientes eléctricas, no obstante, no son la única causa de campo magnético; los dipolos magnéticos inherentes a cada partícula, también generan campos magnéticos.

2 Campo producido por una carga en movimiento

Para una carga puntual que se encuentra instantáneamente en el punto 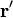$\mathbf{r}'$ moviéndose con velocidad instantánea $\mathbf{v}'$ , mucho menor que la de la luz, el campo magnético que produce en todos los puntos del espacio vale

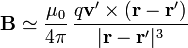
$\mathbf{B}\simeq \frac{\mu_0}{4\pi}\,\frac{q\mathbf{v}'\times(\mathbf{r}-\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|^3}$

siendo $\mathbf{r}_0$ la posición instantánea de la carga.

μ 0

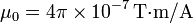es una constante denominada permeabilidad del vacío, cuyo valor en el SI es $\mu_0=4\pi\times 10^{-7}\,\mathrm{T}{\cdot}\mathrm{m}/\mathrm{A}$ .

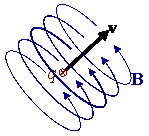
El campo de una carga en movimiento describe circunferencias en torno al movimiento de la carga

2.1 El magnetismo y la 3ª ley de Newton

Combinando la ecuación anterior con la ley de Lorentz resulta para la fuerza magnética que la carga 1 (en movimiento) produce sobre la 2 (también en movimiento) la expresión

$\mathbf{F}_{\mathrm{m}21} = \frac{\mu _0}{4\pi}\,\frac{q_1q_2\mathbf{v}_2 \times \left(\mathbf{v}_1 \times \left(\mathbf{r}_2 - \mathbf{r}_1 \right) \right)}{\left|\mathbf{r}_2 - \mathbf{r}_1 \right|^3}$

Esta fuerza es extraña porque no verifica el principio de acción y reacción

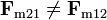
$\mathbf{F}_{\mathrm{m}21} \neq \mathbf{F}_{\mathrm{m}12}$

Esta ley es necesaria para que se conserve la cantidad de movimiento, 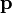$\mathbf{p}$ , ¿cómo se explica el cambio en 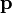$\mathbf{p}$ ? Incluyendo una cantidad de movimiento, 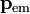$\mathbf{p}_\mathrm{em}$ , del propio campo electromagnético, de forma que

$\mathbf{p}_1+\mathbf{p}_2+\mathbf{p}_\mathrm{em}=\mathrm{cte.}$

En el caso de que se trate del campo magnético de corrientes estacionarias sí se cumple la 3ª ley de Newton, sin necesidad de términos adicionales

2.2 Fuerza entre dos cargas en movimiento paralelo

Supongamos dos cargas

q 1

y

q 2

que se mueven paralelamente con la misma velocidad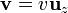 $\mathbf{v} = v\mathbf{u}_z$ sobre rectas separadas una distancia 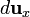$d\mathbf{u}_x$ . El campo de la 1ª en la posición de la 2ª es $\mathbf{B}_1\left(\mathbf{r}_2\right) = \frac{\mu _0q_1v_1}{4\pi d^2}\mathbf{u}_y$

La fuerza magnética sobre $q 2$ es

$\mathbf{F}_{\mathrm{m}21} = q_2\mathbf{v}_2 \times \mathbf{B}_1\left(\mathbf{r}_2\right) = - \frac{\mu _0q_1q_2v^2}{4\pi d^2}\mathbf{u}_x$

La fuerza magnética es atractiva si las cargas son del mismo signo.

Podemos comparar la magnitud de esta fuerza con la fuerza eléctrica entre ambas cargas. Si la velocidad de las cargas es pequeña, podemos aproximar la fuerza mediante la ley de Coulomb:

$\mathbf{F}_{\mathrm{e}21} = \frac{q_1q_2}{4\pi\varepsilon_0d^2}\mathbf{u}_x$

La proporción entre ambas fuerzas es

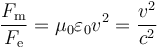
$\frac{F_\mathrm{m}}{F_\mathrm{e}}=\mu_0\varepsilon_0 v^2=\frac{v^2}{c^2}$

donde 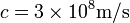$c = 3\times 10^{8}\mathrm{m}/\mathrm{s}$ es la velocidad de la luz. Por ello, normalmente

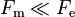
$F_\mathrm{m}\ll F_\mathrm{e}$

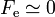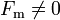Las fuerzas magnéticas sólo son apreciables porque la materia es neutra. En la interacción entre dos hilos conductores de corriente, las fuerzas eléctricas entre iones y electrones se cancelan (y $F_\mathrm{e}\simeq 0$ ). Para la fuerza magnética sólo cuentan los electrones móviles, y $F_\mathrm{m}\neq 0$ .

Una observación más sobre esta fuerza magnética y su relación con la eléctrica. Al hablar del campo magnético producido por una carga puntual se introduce su velocidad, y en la fuerza de Lorentz aparece otra velocidad. la pregunta inmediata es ¿velocidad respecto a qué? No es la velocidad relativa de una carga respecto a la otra (ya que en este ejemplo, las dos cargas se mueven del mismo modo), sino la velocidad respecto a un sistema de referencia fijo. Ahora bien, una de las enseñanzas de la teoría de la relatividad es que no existen los sistemas de referencia absolutos. Si cambiamos de sistema de referencia absoluto resulta que la fuerza magnética valdrá más o menos o incluso anularse. Este comportamiento claramente no relativista de la fuerza magnética no puede ser correcto.

La expresión correcta de la fuerza electromagnética requiere meterse en las honduras de la relatividad especial, por lo que sólo indicaremos dos detalles:

Lo que tiene significado es la fuerza total, suma de la fuerza magnética y de la eléctrica

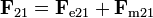
$\mathbf{F}_{21}=\mathbf{F}_{\mathrm{e}21}+\mathbf{F}_{\mathrm{m}21}$

La fuerza eléctrica también depende de la velocidad de las cargas (la ley de Coulomb es solo una aproximación), de forma que al cambiar de sistema de referencia no solo cambia la fuerza magnética, sino también la eléctrica (en una cantidad similar), de manera que la resultante sí se transforma como debe hacerlo una fuerza relativista.

3 Campo creado por una distribución de corriente

3.1 Ley de Biot y Savart

Sumando las contribuciones de los campos creados por cada una de las cargas individuales, resulta la expresión para el campo creado por una distribución de cargas puntuales

$\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\sum_i \frac{q_i\mathbf{v}_i \times \left(\mathbf{r} - \mathbf{r}_i\right)}{\left| \mathbf{r} - \mathbf{r}_i\right|^3}$

A partir de aquí se obtiene el campo debido a una corriente de volumen

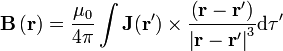
$\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\int \mathbf{J}(\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}\mathrm{d}\tau'$

Análogamente para el caso de una distribución de corriente superficial

$\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\int \mathbf{K}(\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}\mathrm{d}S'$

y para una corriente lineal

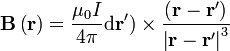
$\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0I}{4\pi}\mathrm{d}\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}$

o para una superposición de ellas

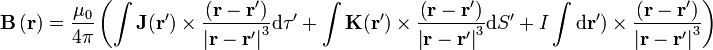
$\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0}{4\pi}\left(\int \mathbf{J}(\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}\mathrm{d}\tau'+\int \mathbf{K}(\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}\mathrm{d}S'+I\int\mathrm{d}\mathbf{r}')\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}\right)$

Todas estas expresiones se denominan indistintamente Ley de Biot y Savart

La ley de Biot y Savart para una distribución volumétrica se deduce de la de un conjunto de cargas puntaules del mismo modo que la ley de Lorentz para una corriente de volumen se obtiene de la de una carga. La ley de Biot y Savart para una corriente lineal se deduce de la de una corriente de volumen de la misma forma que la ley de Lorentz para una corriente lineal se deduce de la de una de volumen.

3.2 Fuerza entre corrientes

Dadas dos distribuciones lineales, la fuerza entre ellas será:

$\mathbf{F}_{I'\to I}=\frac{\mu_0II'}{4\pi}\int_{\Gamma}\int_{\Gamma'}\frac{\mathrm{d}\mathbf{r}\times(\mathrm{d}\mathbf{r}\times(\mathbf{r}-\mathbf{r}'))}{|\mathbf{r}-\mathbf{r}'|^3}$

Esta fórmula también se conoce como Ley de Biot y Savart. Predice que corrientes paralelas (↑↑) se atraen, mientras que las antiparalelas (↑↓) se repelen.

3.3 Campo de una espira circular

Artículo completo: Campo magnético de una espira circular

Supongamos una espira circular por la cual circula una corriente $I$ . Se trata de hallar el campo magnético en los puntos del eje de la espira (para el resto del espacio no existe expresión analítica sencilla)

Aplicamos la ley de Biot y Savart

Tomamos como eje z el de la espira, de forma que

$\mathbf{r} = z\mathbf{u}_z\,$ $\mathbf{r}' = R\left(\cos\varphi'\,\mathbf{u}_x + \,\mathrm{sen}\,\varphi'\,\mathbf{u}_y\right)$ $\mathrm{d}\mathbf{r}' = R\left(-\,\mathrm{sen}\,\varphi'\,\mathbf{u}_x + \cos\varphi'\,\mathbf{u}_y \right)\mathrm{d}\varphi '$

$\mathbf{r} - \mathbf{r}' = - R\cos\varphi'\,\mathbf{u}_x - R\,\mathrm{sen},\varphi'\,\mathbf{u}_y + z\mathbf{u}_z$ $\left|\mathbf{r} - \mathbf{r}'\right| = \sqrt{R^2 + z^2}$

Hallando el producto vectorial y extrayendo los factores constantes:

$\mathbf{B}(z) = \frac{\mu _0IR}{4\pi\left(R^2 + z^2\right)^{3/2}}\left(\mathbf{u}_xz\int_0^{2\pi} \cos\varphi'\,\mathrm{d}\varphi' + \mathbf{u}_yz\int_0^{2\pi}\mathrm{sen}\,\varphi'\mathrm{d}\varphi' + \mathbf{u}_zR\int_0^{2\pi} \mathrm{d}\varphi'\right)$

3.4 Campo de una corriente rectilínea

Artículo completo: Campo magnético de una corriente rectilínea

Campo magnético debido a una corriente

De Laplace

Contenido

1 Introducción

2 Campo producido por una carga en movimiento

2.1 El magnetismo y la 3ª ley de Newton

2.2 Fuerza entre dos cargas en movimiento paralelo

3 Campo creado por una distribución de corriente

3.1 Ley de Biot y Savart

3.2 Fuerza entre corrientes

3.3 Campo de una espira circular

3.4 Campo de una corriente rectilínea

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES