Los gases ideales (GIOI)

De Laplace

Revisión a fecha de 13:29 3 mar 2021; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Ecuación de estado
2 Gases no ideales. Compresibilidad
3 Trabajo, calor y energía
4 Coeficientes termodinámicos
- 4.1 Coeficiente de dilatación térmica
- 4.2 Coeficiente de compresibilidad isoterma
5 Entropía de un gas ideal

1 Ecuación de estado

1.1 Ley de Boyle

La ley de Boyle (también conocida como ley de Boyle y Mariotte), nos dice que si en un gas ideal se mantiene la temperatura constante, la presión del gas es inversamente proporcional al volumen que ocupa, lo que se expresa

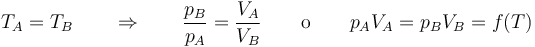
$T_A = T_B\qquad\Rightarrow\qquad \frac{p_B}{p_A}=\frac{V_A}{V_B}\qquad \mbox{o}\qquad p_AV_A = p_BV_B=f(T)$

Si aquí introducimos magnitudes específicas, dividiendo por la masa de gas, nos queda

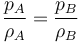
$\frac{p_A}{\rho_A} = \frac{p_B}{\rho_B}$

o, equivalentemente, que la densidad de un gas ideal es proporcional a su presión, a temperatura constante

$p = f(T)\rho\qquad\qquad pV = F(T)$

con $F (T)$ una cierta función de la temperatura y proporcional a la masa de gas.

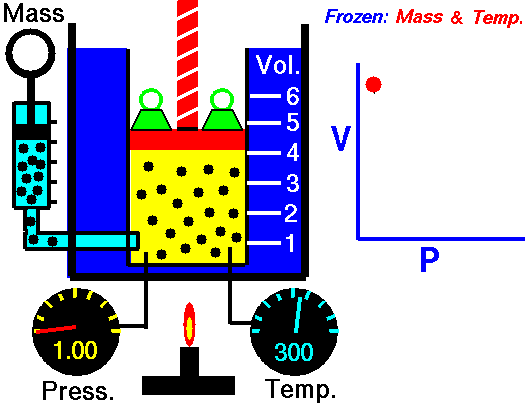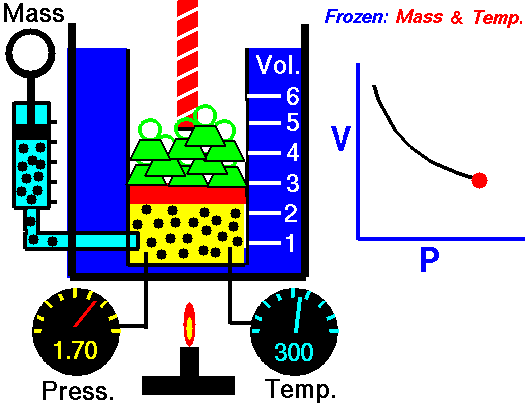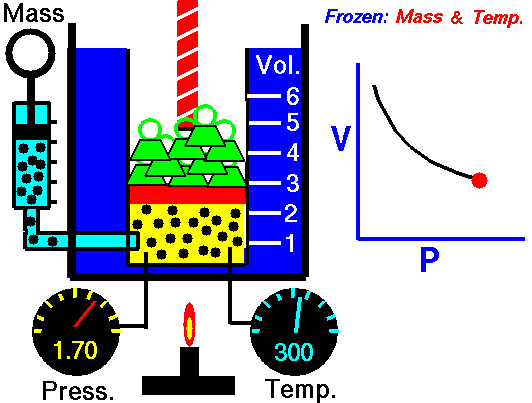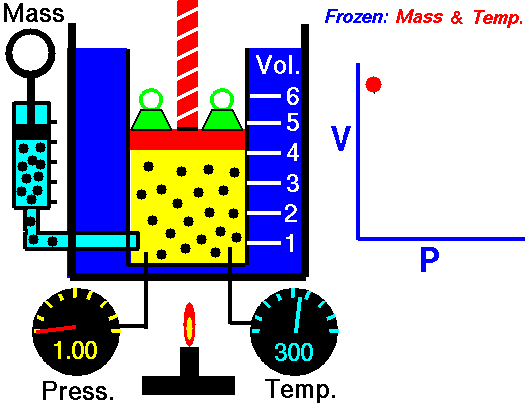
1.2 Ley de Charles

La ley de Charles (también llamada de Gay-Lussac, de Charles y Gay-Lussac, o de los volúmenes) afirma que en un gas ideal a presión constante, el volumen que ocupa el gas varía linealmente con la temperatura que tiene

$p_1=p_2\qquad\Rightarrow\qquad V(t) = A + B t_C\,$

o equivalentemente, que la temperatura de un gas ideal varía linealmente con el volumen que ocupa

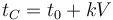
$t_C = t_0+k V\,$

Experimentalmente se encuentra que la ordenada $t 0$ , que representaría la temperatura a la cual el gas ideal ocuparía un volumen nulo (aunque ningún gas se puede llevar hasta esa temperatura), es independiente de la presión del gas siempre que sea baja y vale aproximadamente 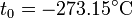$t_0=-273.15^\circ\mathrm{C}$ . Definiendo entonces la temperatura absoluta del gas como

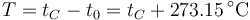
$T = t_C - t_0 = t_C+273.15\,^\circ\mathrm{C}$

la ley de Charles se escribe

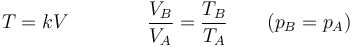
$T = kV\qquad\qquad\frac{V_B}{V_A}=\frac{T_B}{T_A}\qquad (p_B=p_A)$

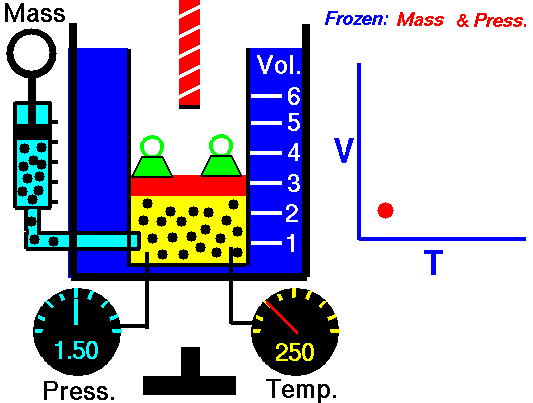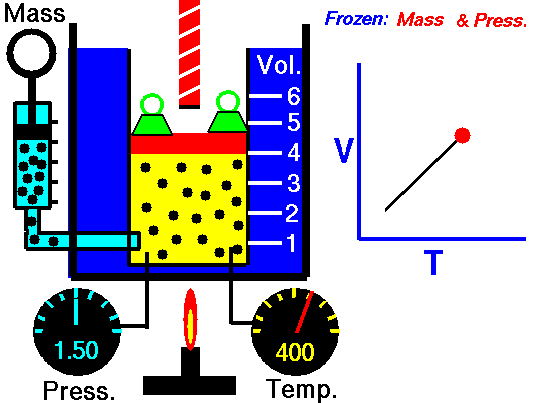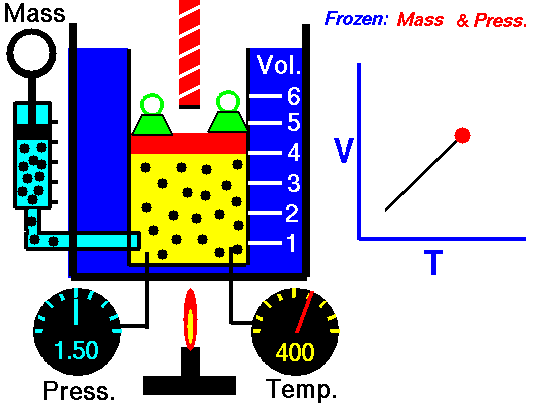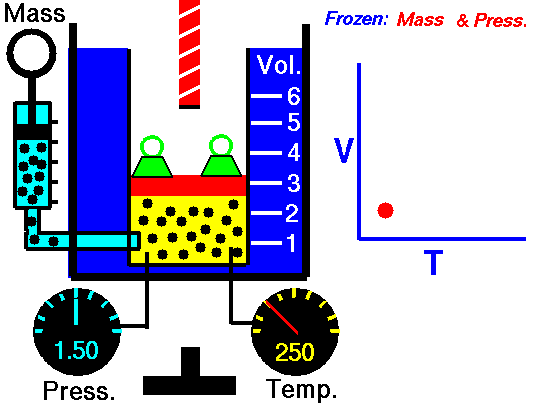
1.3 Ecuación general

Combinando la ley de Charles con la de Boyle obtenemos, para un sistema cerrado en el que la masa de gas permanece constante,

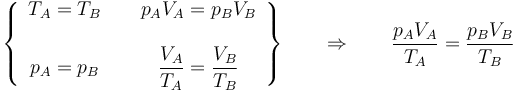
$\left\{\begin{array}{ccc}T_A=T_B&\ & p_AV_A=p_BV_B \\ && \\ p_A=p_B & \ & \displaystyle\frac{V_A}{T_A}=\displaystyle \frac{V_B}{T_B}\end{array}\right\}\qquad\Rightarrow\qquad \frac{p_AV_A}{T_A}=\frac{p_BV_B}{T_B}$

o, equivalentemente,

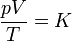
$\frac{pV}{T}=K$

siendo K una constante específica para cada muestra de gas y que no depende ni de la presión, ni del volumen, ni de la temperatura. Puesto que el primer miembro es una cantidad extensiva (el volumen es proporcional a la masa), el segundo miembro también debe serlo, por lo que puede escribirse en la forma

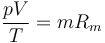
$\frac{pV}{T}=mR_m$

siendo $R m$ una constante diferente para cada gas (constante del gas).

Una tabla de valores, tomada de toolbox sería la siguiente:

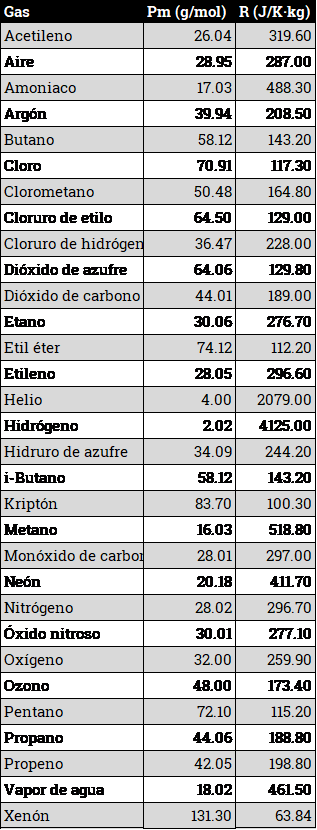
Si a partir de la tabla anterior se representa la constante de cada gas en función del peso molecular, podemos ver, mediante una escala logarítmica, que esa constante es, muy aproximadamente, inversamente proporcional al peso molecular

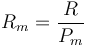
$R_m=\frac{R}{P_m}$

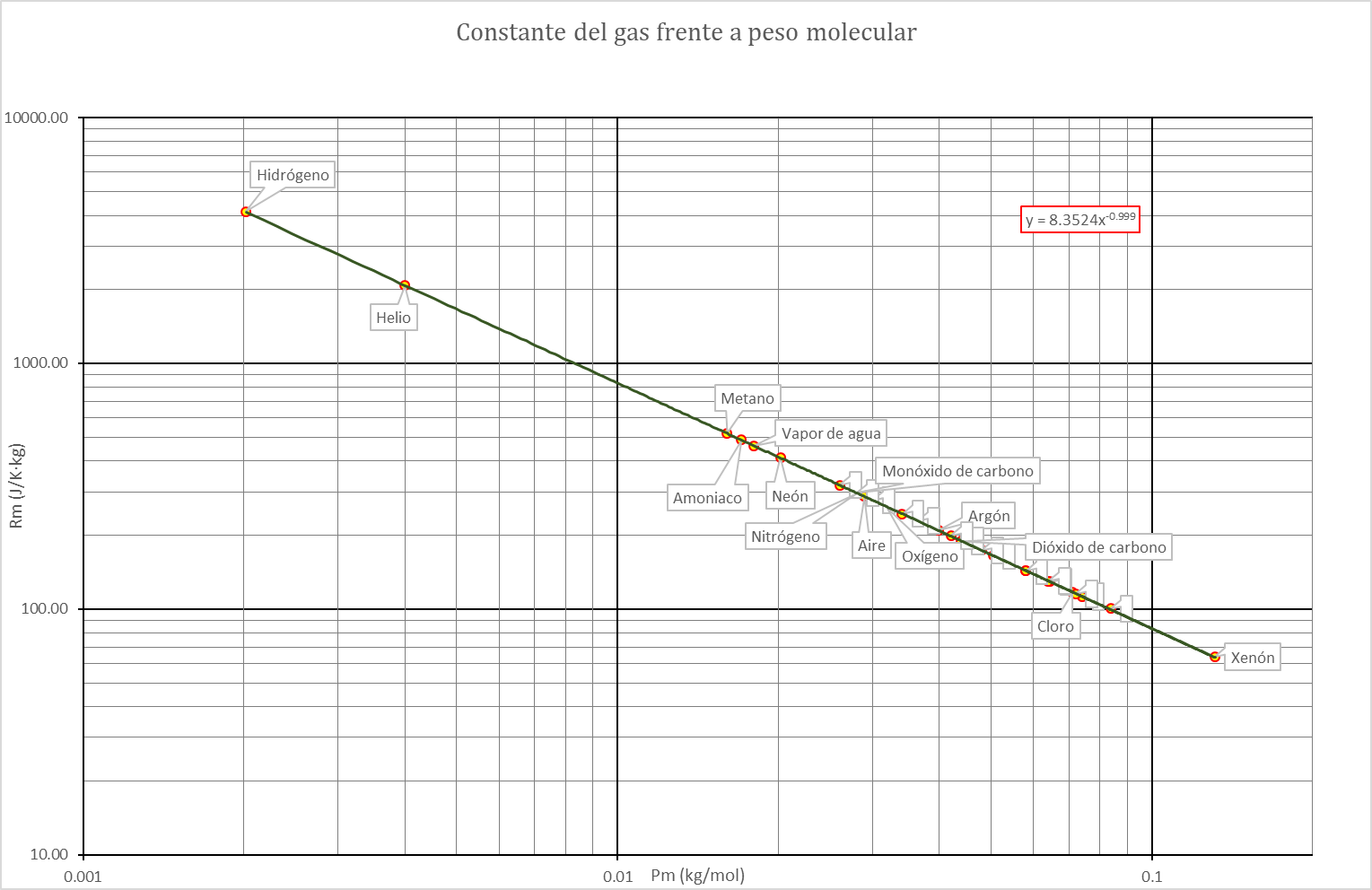
Podemos escribir la ley de los gases ideales como una relación entre magnitudes intensivas dividiendo por el volumen

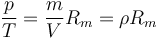
$\frac{p}{T}=\frac{m}{V}R_m =\rho R_m$

o, dicho de otra forma, que la densidad de un gas es directamente proporcional a su presión e inversamente proporcional a su temperatura

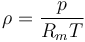
$\rho=\frac{p}{R_mT}$

1.3.1 Gases puros

Para un gas puro, constituido por un solo tipo de moléculas, la ley de los gases ideales puede escribirse en función del número de moles

$n=\frac{m}{P_m}\qquad\Rightarrow\qquad \frac{pV}{T}= n P_mR_m$

siendo $P m$ el peso molecular. Según se ha indicado, se encuentra experimentalmente que el producto

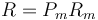
$R=P_mR_m\,$

es prácticamente independiente del gas de que se trate. Por ello, a la constante $R$ se la denomina constante universal de los gases ideales. De esta forma, queda la ecuación general

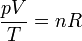
$\frac{pV}{T}=nR$

El valor de $R$ en el SI es

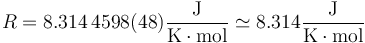
$R = 8.314\,4598(48)\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}\simeq 8.314\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}$

Esta ecuación de estado suele escribirse en la forma

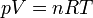
$pV = nRT\,$

1.3.2 Mezclas ideales de gases ideales. El aire seco

Las mezclas de gases, como el aire seco (sin vapor de agua), no son sustancias puras, sino que combinan diferentes tipos de moléculas. Por ello, aunque cumplen la ley de los gases ideales

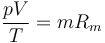
$\frac{pV}{T}=mR_m$

con

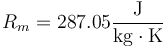
$R_m = 287.05\frac{\mathrm{J}}{\mathrm{kg}\cdot\mathrm{K}}$

para el aire seco, no es trivial pasar esta expresión a número de moles, ya que ¿qué es un mol de aire? No podemos multiplicar la constante por el peso molecular del aire, pues no está definido en principio (¿es el del nitrógeno? ¿el del oxígeno? ¿cómo se combinan?). De hecho, podemos emplearla para definir un peso molecular efectivo

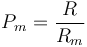
$P_m=\frac{R}{R_m}$

que nos da, para el aire seco,

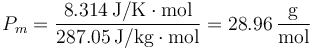
$P_m=\frac{8.314\,\mathrm{J}/\mathrm{K}\cdot\mathrm{mol}}{287.05\,\mathrm{J}/\mathrm{kg}\cdot\mathrm{mol}}=28.96\,\frac{\mathrm{g}}{\mathrm{mol}}$

Ahora bien, podemos llegar al peso molecular efectivo de otra forma.

En una mezcla ideal de gases ideales, no solo se comporta idealmente cada gas por separado, sino que no interactúan entre sí. En ese caso, cada molécula se mueve independientemente y los choques que puedan tener con las paredes no dependen del resto de sustancias. Por tanto la presión resultante es la suma de las presiones parciales, que son las que producirían los distintos gases si estuvieran solos en el recipiente

$p=\sum_i p_i\,\qquad\qquad p_i = \frac{n_i R T}{V}$

Como cada gas es ideal y la temperatura de cada uno y el volumen que ocupa es el mismo para todos

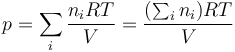
$p=\sum_i \frac{n_i R T}{V}=\frac{(\sum_i n_i)RT}{V}$

Comparando con la ecuación de los gases ideales para una sustancia pura, podemos definir el número de moles de aire como

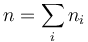
$n=\sum_i n_i\,$

Por otro lado, la masa total del aire es la suma de las de los gases constituyentes

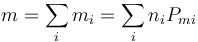
$m=\sum_i m_i = \sum_i n_i P_{mi}\,$

lo que nos permite definir el peso molecular del aire como

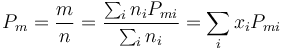
$P_m=\frac{m}{n}=\frac{\sum_i n_iP_{mi}}{\sum_i n_i}=\sum_i x_iP_{mi}$

siendo $x i$ la fracción molar del gas i

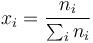
$x_i=\frac{n_i}{\sum_i n_i}$

Aplicando esto al caso del aire seco, que tiene una fracción molar de 78.1% de N2, 20.9% de O2 y 1.0% de Ar (más otros gases en fracciones menores) resulta un peso molecular efectivo

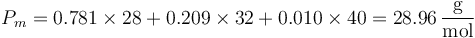
$P_m = 0.781\times 28+0.209\times 32 + 0.010\times 40 = 28.96\,\frac{\mathrm{g}}{\mathrm{mol}}$

de acuerdo con el otro cálculo.

1.4 Aplicaciones. Termómetro a volumen constante

Enlace al artículo sobre temperatura absoluta.

2 Gases no ideales. Compresibilidad

El modelo del gas ideal es válido para gases poco densos a baja presión. Sin embargo, para situaciones que se alejan de estas condiciones es preciso hacer correcciones al modelo.

Una forma de medir la no idealidad es mediante el factor de compresibilidad,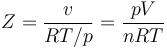

Z

. Este factor se define como el cociente entre el volumen molar real de un gas (

v = V / n

)y el que debería tener si fuera válida la ley de los gases ideales $Z = \frac{v}{RT/p} = \frac{pV}{nRT}$

Para un gas ideal obviamente $Z = 1$ pero para uno real, cuanto más se aleje Z de la unidad, menos válido será el modelo de gas ideal.

Cuando tenemos un gas real es necesario emplear ecuaciones más complejas para describir su comportamiento.

Una de estas es la ecuación de Van der Waals

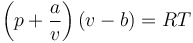
$\left(p+\frac{a}{v}\right)(v-b)=RT$

donde el volumen se corrige teniendo en cuenta el espacio ocupado por las moléculas y el aumento de la presión debido a las fuerzas entre moléculas. Esta ecuación predice comportamientos que no aparecen en el gas ideal, como el cambio de fase a líquido.

Los valores de las constantes $a$ y $b$ pueden determinarse experimentalmente a partir de las medidas del factor de compresibilidad.

Otra posible mejora consiste en sustituir la ecuación del gas ideal por una serie cuyos sucesivos coeficientes se determinan experimentalmente o por métodos analíticos. Así tenemos la ecuación del virial

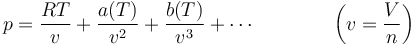
$p=\frac{RT}{v} +\frac{a(T)}{v^2}+\frac{b(T)}{v^3} + \cdots\qquad\qquad \left(v=\frac{V}{n}\right)$

en la que los coeficientes $a (T)$ , $b (T)$ se determinan a partir de las propiedades del gas real.

3 Trabajo, calor y energía

Como todo sistema termodinámico, sobre un gas se puede realizar trabajo e introducir calor, variando su energía interna

3.1 Trabajo

El trabajo sobre un gas se realiza variando el volumen que ocupa. Consideremos un cilindro con un pistón de área $S$ . Cuando sobre este pistón se ejerce una fuerza normal $F$ el pistón se desplaza una cantidad $d x$ . En este proceso se realiza un trabajo diferencial

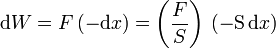
$\mathrm{d}W=F\,(-\mathrm{d}x) = \left(\frac{F}{S}\right)\,(-\mathrm{S}\,\mathrm{d}x)$

El signo negativo en $- d x$ se debe a que el trabajo realizado sobre el gas es positivo cuando el gas se comprime y el émbolo se desplaza hacia el interior del gas. En la última ecuación el primer factor es la presión ejercida sobre el émbolo, mientras que el segundo es la disminución de volumen del gas. Por tanto, el trabajo diferencial es igual a

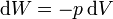
$\mathrm{d}W=-p\,\mathrm{d}V$

Hay que destacar que en esta expresión $p$ es la presión exterior, no la propia del gas. Sólo en procesos cuasiestáticos en que la presión interior iguala prácticamente a la exterior, se podrá sustituir una por otra.

3.2 Energía interna

En principio, la energía interna de un gas puede depender de su temperatura y de su volumen (por ser dos variables independientes). Sin embargo, Joule descubrió que para un gas aproximadamente ideal, la energía interna no depende del volumen, sino solo de su temperatura.

$U=U(T)\,$

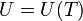
La experiencia de Joule consistió en medir la temperatura de un gas, someterlo a una expansión brusca en el vacío rompiendo un diafragma, y volver a medir la temperatura. Por no haber presión exterior el trabajo es nulo. Por ser una expansión brusca el proceso es prácticamente adiabático y no hay calor transferido al sistema. Por tanto, la energía interna del gas permanece constante

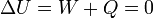
$\Delta U = W + Q = 0\,$

Cuando midió la temperatura final, Joule obtuvo que su valor era prácticamente igual a la inicial. Puesto que la temperatura no cambia, pero el volumen sí, y resulta que la energía interna permanece constante, se llega a la conclusión de que U no depende del volumen y sólo es función de la temperatura.

3.3 Procesos en un gas ideal

Enlace al artículo sobre trabajo en termodinámica.

4 Coeficientes termodinámicos

Cuando se tiene una ecuación de estado sencilla, es posible calcular analíticamente los diferentes coeficientes termodinámicos.

4.1 Coeficiente de dilatación térmica

Nos da cómo varía relativamente el volumen con el incremento de temperatura

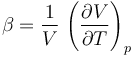
$\beta = \frac{1}{V}\,\left(\frac{\partial V}{\partial T}\right)_p$

Sustituyendo aquí la ley de los gases ideales

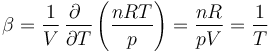
$\beta = \frac{1}{V}\,\frac{\partial\ }{\partial T}\left(\frac{nRT}{p}\right)=\frac{nR}{pV}=\frac{1}{T}$

es decir, es igual a la inversa de la temperatura absoluta. Puesto que el coeficiente de dilatación puede medirse experimentalmente, fue de esta forma como se determinó por primera vez la temperatura Celsius del cero absoluto.

4.2 Coeficiente de compresibilidad isoterma

Mide cómo disminuye un volumen (o aumenta la densidad) cuando se comprime una sustancia, manteniendo constante la temperatura.

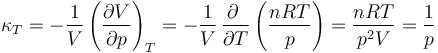
$\kappa_T = -\frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_T = -\frac{1}{V}\,\frac{\partial\ }{\partial T}\left(\frac{nRT}{p}\right)=\frac{nRT}{p^2V}=\frac{1}{p}$

5 Entropía de un gas ideal

Enlace al artículo sobre entropía.

Los gases ideales (GIOI)

De Laplace

Contenido

1 Ecuación de estado

1.1 Ley de Boyle

1.2 Ley de Charles

1.3 Ecuación general

1.3.1 Gases puros

1.3.2 Mezclas ideales de gases ideales. El aire seco

1.4 Aplicaciones. Termómetro a volumen constante

2 Gases no ideales. Compresibilidad

3 Trabajo, calor y energía

3.1 Trabajo

3.2 Energía interna

3.3 Procesos en un gas ideal

4 Coeficientes termodinámicos

4.1 Coeficiente de dilatación térmica

4.2 Coeficiente de compresibilidad isoterma

5 Entropía de un gas ideal

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES