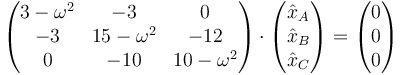Tres masas unidas por resortes (CMR)

De Laplace

Revisión a fecha de 20:23 31 dic 2020; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Ecuaciones de movimiento
3 Modos normales
4 Solución particular

1 Enunciado

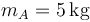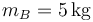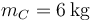Se tienen tres masas, de valores $m_A=5\,\mathrm{kg}$ , $m_B=5\,\mathrm{kg}$ y $m_C=6\,\mathrm{kg}$ se hallan unidas por resortes. Entre la A y la B se encuentra uno de constante 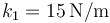$k_1=15\,\mathrm{N}/\mathrm{m}$ y longitud natural 10cm, y entre la B y la C uno de constante 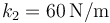$k_2=60\,\mathrm{N}/\mathrm{m}$ y longitud natural 10cm. Inicialmente se encuentran las tres masas en reposo y los muelles en su longitud natural. 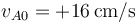Entonces se le comunica a la masa A una velocidad inicial $v_{A0}=+16\,\mathrm{cm}/\mathrm{s}$ .

Determine la posición de cada masa como función del tiempo.

2 Ecuaciones de movimiento

En lo que sigue se usarán todas las magnitudes en las unidades fundamentales del SI.

Dado un sistema de referencia fijo, las posiciones de las tres partículas serán, respectivamente $X A (t)$ , $X B (t)$ y $X C (t)$ . Por comodidad, definimos las variables

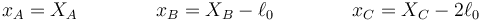
$x_A=X_A\qquad\qquad x_B = X_B-\ell_0\qquad\qquad x_C=X_C-2\ell_0$

siendo 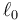$\ell_0$ la longitud natural de ambos resortes. De esta manera podemos describir el movimiento como las desviaciones respecto a posiciones de equlibrio y podemos tratar los resortes como si tuvieran longitud natural nula.

Las ecuaciones de movimiento las da la segunda ley de Newton. Para la primera masa

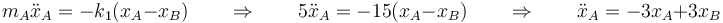
$m_A\ddot{x}_A=-k_1(x_A-x_B)\qquad\Rightarrow\qquad 5\ddot{x}_A=-15(x_A-x_B)\qquad\Rightarrow\qquad \ddot{x}_A=-3x_A+3x_B$

Para la segunda

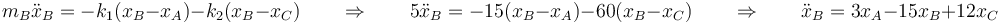
$m_B\ddot{x}_B=-k_1(x_B-x_A)-k_2(x_B-x_C)\qquad\Rightarrow\qquad 5\ddot{x}_B=-15(x_B-x_A)-60(x_B-x_C)\qquad\Rightarrow\qquad \ddot{x}_B=3x_A-15x_B+12x_C$

y para la tercera

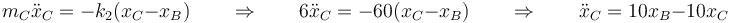
$m_C\ddot{x}_C=-k_2(x_C-x_B)\qquad\Rightarrow\qquad 6\ddot{x}_C=-60(x_C-x_B)\qquad\Rightarrow\qquad \ddot{x}_C=10x_B-10x_C$

Por tanto, el sistema de ecuaciones de movimiento es

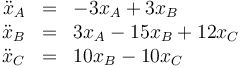
$\begin{array}{rcl} \ddot{x}_A&=&-3x_A+3x_B\\ \ddot{x}_B&=&3x_A-15x_B+12x_C\\ \ddot{x}_C&=&10x_B-10x_C \end{array}$

con las condiciones iniciales

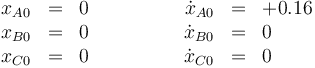
$\begin{array}{rcl} x_{A0}&=&0\\ x_{B0}&=&0\\ x_{C0}&=&0 \end{array}\qquad\qquad \begin{array}{rcl} \dot{x}_{A0}&=&+0.16\\ \dot{x}_{B0}&=&0\\ \dot{x}_{C0}&=&0 \end{array}$

3 Modos normales

El sistema de ecuaciones de movimiento puede escribirse en forma matricial como

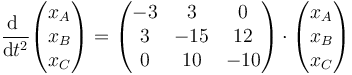
$\frac{\mathrm{d}\ }{\mathrm{d}t^2}\begin{pmatrix}x_A\\x_B\\x_C\end{pmatrix}=\begin{pmatrix}-3&3&0\\3&-15&12\\0&10&-10\end{pmatrix}\cdot \begin{pmatrix}x_A\\x_B\\x_C\end{pmatrix}$

Existen diferentes formas de resolver este sistema de ecuaciones diferenciales de coeficientes constantes.

Una de ellas consiste en buscar los llamados modos normales, que son oscilaciones del sistema con una frecuencia completa, de forma que la solución puede escribirse en la forma

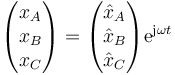
$\begin{pmatrix}x_A\\x_B\\x_C\end{pmatrix} = \begin{pmatrix}\hat{x}_A\\\hat{x}_B\\\hat{x}_C\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega t}$

Una solución de este tipo no cumplirá, en general, las condiciones iniciales. Sin embargo, puede demostrarse que la solución general es una combinación lineal de los diferentes modos normales. El problema se traslada entonces a encontrar los coeficientes adecuados para cada caso concreto.

Veamos primero cuáles son los modos normales en este caso. Sustituyendo la solución propuesta la ecuación diferencial se transforma en la ecuación algebraica

$-\omega^2\begin{pmatrix}\hat{x}_A\\\hat{x}_B\\\hat{x}_C\end{pmatrix}=\begin{pmatrix}-3&3&0\\3&-15&12\\0&10&-10\end{pmatrix}\cdot \begin{pmatrix}\hat{x}_A\\\hat{x}_B\\\hat{x}_C\end{pmatrix}$

o, agrupando términos,

$\begin{pmatrix}3-\omega^2&-3&0\\-3&15-\omega^2&-12\\0&-10&10-\omega^2\end{pmatrix}\cdot \begin{pmatrix}\hat{x}_A\\\hat{x}_B\\\hat{x}_C\end{pmatrix}=\begin{pmatrix}0\\0\\0\end{pmatrix}$

Tres masas unidas por resortes (CMR)

De Laplace

Contenido

1 Enunciado

2 Ecuaciones de movimiento

3 Modos normales

4 Solución particular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES