Primera Prueba de Control 2020/21 (MR G.I.C.)
De Laplace
1 Cilindro rodando sin deslizar
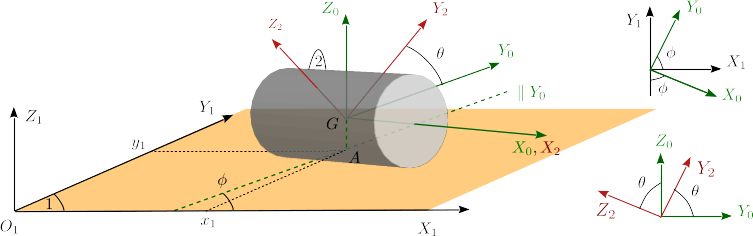
Un cilindro de radio R (sólido "2") rueda sin deslizar sobre un plano fijo O1X1Y1Z1 (sólido "1"). Los ejes GX2Y2Z2 son solidarios con el cilindro. Introducimos unos ejes auxiliares GX0Y0Z0 que cumplen las siguientes propiedades: el X0 es paralelo al eje del cilindro; el eje Z0 es perpendicular al plano fijo "1"; el ángulo que forma el eje Y0 con el eje X1 es φ. El punto A señala el punto geométrico en la vertical de G donde el cilindro está en contacto con el plano. Las coordenadas de este punto en los ejes "1" son x1, y1. Estas son también las coordenadas de G en el plano fijo. Los diagramas auxiliares indican los ángulos relevantes entre los diferentes sistemas de ejes.
- Encuentra la reducción cinemática en el punto G de los movimientos {01}, {20}, {21}. Expresa los resultados en la base "0" y usa el menor número de coordenadas posible.
2. Si el tensor de inercia del cilindro en G es de la forma
![\overleftrightarrow{I_O}
=
\left[
\begin{array}{ccc}
I_{1} & 0 & 0 \\
0 & I_{2} & 0 \\
0 & 0 & I_{2}
\end{array}
\right]](/wiki/images/math/8/f/3/8f3682532f8b4882ceeef260909de880.png)
con I1, I2 conocidos, calcula el momento cinético del cilindro en G y su energía cinética.
2 Tensor de inercia de un hexágono
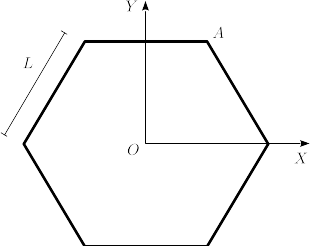
EL sólido rígido de la figura es un hexágono de lado L. Cada lado del hexágono tiene una masa m.
- Calcula el tensor de inercia del hexágono en su centro, expresado en los ejes de la figura..
- Calcula el tensor de inercia en el vértice A, expresado en los mismos ejes.
- Calcula el momento de inercia respecto a un eje paralelo al eje OX y que pase por A.
3 Movimiento instantáneo de barras articuladas
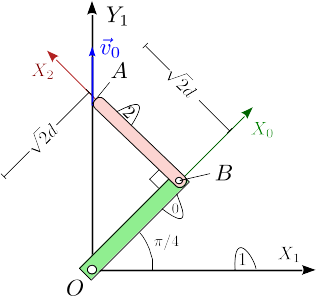
Una barra delgada (sólido “0”), de longitud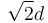 
, está articulada en un punto fijo O y rota en el plano fijo OX1Y1. Otra barra delgada (sólido “2”) de la misma longitud se articula en su punto B en en el extremo de la barra “0”. El punto A de la barra “2” desliza sobre el eje OY1 con una velocidad v0 . Los cálculos que se piden a continuación corresponden al instante indicado en la figura. En ese instante las dos barras son perpendiculares.
- Determina gráfica y analíticamente la posición de los C.I.R. de los movimientos {01}, {20} y {21}
- Calcula una reducción cinemática de esos movimientos.
- Si la velocidad absoluta del punto A es constante en el tiempo, calcula las derivadas temporales de esas reducciones cinemáticas.
