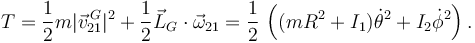Entrar Página Discusión Historial Go to the site toolbox

Cilindro rodando sin deslizar (Dic. 2020)

De Laplace

Contenido

[ocultar]

1 Enunciado

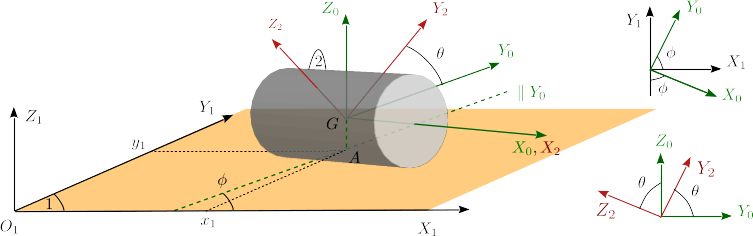
Un cilindro de radio R (sólido "2") rueda sin deslizar sobre un plano fijo O1X1Y1Z1 (sólido "1"). Los ejes GX2Y2Z2 son solidarios con el cilindro. Introducimos unos ejes auxiliares GX0Y0Z0 que cumplen las siguientes propiedades: el X0 es paralelo al eje del cilindro; el eje Z0 es perpendicular al plano fijo "1"; el ángulo que forma el eje Y0 con el eje X1 es φ. El punto A señala el punto geométrico en la vertical de G donde el cilindro está en contacto con el plano. Las coordenadas de este punto en los ejes "1" son x1, y1. Estas son también las coordenadas de G en el plano fijo. Los diagramas auxiliares indican los ángulos relevantes entre los diferentes sistemas de ejes.

  1. Encuentra la reducción cinemática en el punto G de los movimientos {01}, {20}, {21}. Expresa los resultados en la base "0" y usa el menor número de coordenadas posible.

2. Si el tensor de inercia del cilindro en G es de la forma

\overleftrightarrow{I_O} = \left[ \begin{array}{ccc} I_{1} & 0 & 0 \\ 0 & I_{2} & 0 \\ 0 & 0 & I_{2} \end{array} \right]

con I1, I2 conocidos, calcula el momento cinético del cilindro en G y su energía cinética.

2 Solución

2.1 Reducciones cinemáticas en G

De la lectura atenta del enunciado deducimos los siguientes datos cinemáticos:

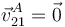  1. \vec{v}^A_{21} = \vec{0}, pues el cilindro rueda sin deslizar sobre el plano "1".
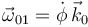  2. \vec{\omega}_{01} = \dot{\phi}\,\vec{k}_0 , pues el eje Y0 forma un ángulo φ con el eje X1.
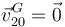  3. \vec{v}^G_{20}=\vec{0}, pues el centro del cilindro (sólido "2") y el origen del sistema de ejes "0" coinciden siempre.
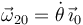  4. \vec{\omega}_{20} = \dot{\theta}\,\vec{\imath}_0, pues el eje Y2 forma un ángulo θ con el eje Y0.

Con esto ya podemos encontrar las reducciones cinemáticas pedidas

2.1.1 Movimiento {21}

Obtenemos \vec{\omega}_{21} de la composición

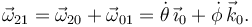
\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = \dot{\theta}\,\vec{\imath}_0 + \dot{\phi}\,\vec{k}_0.

Como ya tenemos 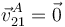\vec{v}^{A}_{21}=\vec{0}, aplicamos Chasles entre los puntos A y G para el movimiento {21}

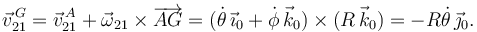
\vec{v}^{\,G}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AG} = (\dot{\theta}\,\vec{\imath}_0 + \dot{\phi}\,\vec{k}_0)\times (R\,\vec{k}_0) = -R\dot{\theta}\,\vec{\jmath}_0.

2.1.2 Movimiento {20}

Este lo tenemos directamente del análisis del enunciado

\vec{\omega}_{20} = \dot{\theta}\,\vec{\imath}_0, \qquad \vec{v}^{\,G}_{20} = \vec{0}.

2.1.3 Movimiento {01}

Tenemos 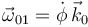\vec{\omega}_{01}=\dot{\phi}\,\vec{k}_0 del análisis del enunciado. Obtenemos la velocidad en G usando las leyes de composición

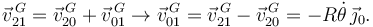
\vec{v}^{\,G}_{21} = \vec{v}^{\,G}_{20} + \vec{v}^{\,G}_{01} \to \vec{v}^{\,G}_{01} = \vec{v}^{\,G}_{21} - \vec{v}^{\,G}_{20} = -R\dot{\theta}\,\vec{\jmath}_0.

La velocidad 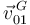\vec{v}^{\,G}_{01} también se puede obtener derivando respecto al tiempo el vector de posición

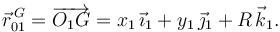
\vec{r}^{\,G}_{01} = \overrightarrow{O_1G} = x_1\,\vec{\imath}_1 + y_1\,\vec{\jmath}_1 + R\,\vec{k}_1.

Este vector de posición se puede derivar porque apunta siempre al centro del cilindro. Haciendo la derivada tenemos

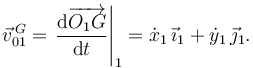
\vec{v}^{\,G}_{01} = \left.\dfrac{\mathrm{d} \overrightarrow{O_1G}}{\mathrm{d}t} \right|_1 = \dot{x}_1\,\vec{\imath}_1 + \dot{y}_1\,\vec{\jmath}_1.

Esta velocidad esta expresada en función de x1 e y1- Hay una ligadura entre estas coordenadas y las coordenadas angulares. Para verla expresamos 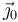\vec{\jmath}_0 en la base "1"

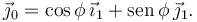
\vec{\jmath}_0 = \cos\phi\,\vec{\imath}_1 + \mathrm{sen}\,\phi\,\vec{\jmath}_1.

Con esto tenemos

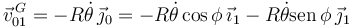
\vec{v}^{\,G}_{01} = -R\dot{\theta}\,\vec{\jmath}_0 = -R\dot{\theta}\cos\phi\,\vec{\imath}_1 -R\dot{\theta}\mathrm{sen}\,\phi\,\vec{\jmath}_1

Comparando las dos expresiones de 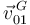\vec{v}^{\,G}_{01} obtenemos

\dot{x}_1 = -R\dot{\theta}\cos\phi, \qquad \dot{y}_1 = -R\dot{\theta}\mathrm{sen}\phi.

2.2 Momento angular y energía cinética

El momento angular respecto al CM es

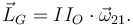
\vec{L}_G = II_O\cdot\vec{\omega}_{21}.

Como el tensor está expresado en la base "2", hay que expresar el vector rotación en esa base. Tenemos

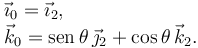
\begin{array}{l} \vec{\imath}_0 = \vec{\imath}_2,\\ \vec{k}_0 = \mathrm{sen}\,\theta\,\vec{\jmath}_2 + \cos\theta\,\vec{k}_2. \end{array}

Entonces

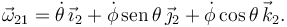
\vec{\omega}_{21} = \dot{\theta}\,\vec{\imath}_2 + \dot{\phi}\,\mathrm{sen}\,\theta\,\vec{\jmath}_2 + \dot{\phi}\cos\theta\,\vec{k}_2.

El momento cinético es

\vec{L}_G = \left[ \begin{array}{ccc} I_{1} & 0 & 0 \\ 0 & I_{2} & 0 \\ 0 & 0 & I_{2} \end{array} \right] \left[ \begin{array}{c} \dot{\theta} \\ \dot{\phi}\,\mathrm{sen}\,\theta \\ \dot{\phi}\cos\theta \end{array} \right]_2 = [I_1\dot{\theta}, I_2 \dot{\phi}\,\mathrm{sen}\,\theta, I_2 \dot{\phi}\cos\theta ]_2.

La energía cinética puede calcularse así

T = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 + \dfrac{1}{2}\vec{L}_G\cdot\vec{\omega}_{21} = \dfrac{1}{2}\, \left( (mR^2+I_1)\dot{\theta}^2 + I_2\dot{\phi}^2 \right).

Obtenido de "http://tesla.us.es/wiki/index.php/Cilindro_rodando_sin_deslizar_(Dic._2020)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace