Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Dos discos III (Ex.Ene/20)

De Laplace

1 Enunciado

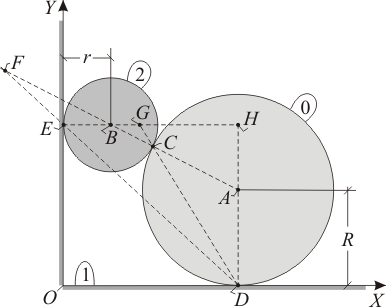
El sistema mecánico de la figura, contenido en todo instante en el plano fijo OXY\, (sólido "1"), está constituido por un disco de centro A\, y radio R\, (sólido "0") que rueda sin deslizar sobre el eje OX\,, y por otro disco de centro B\, y radio r\, (sólido "2") que rueda sin deslizar sobre el eje OY\, a la vez que se mantiene en contacto tangente con el disco anterior.

  1. ¿Cuál de las siguientes igualdades es falsa?
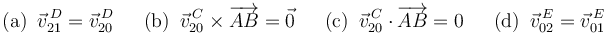
    \mathrm{(a)}\,\,\,\vec{v}^{\, D}_{21}=\vec{v}^{\, D}_{20}\,\,\,\,\,\,\,\,\,\mathrm{(b)}\,\,\,\vec{v}^{\, C}_{20}\times\overrightarrow{AB}=\vec{0}\,\,\,\,\,\,\,\,\,\mathrm{(c)}\,\,\,\vec{v}^{\, C}_{20}\cdot\overrightarrow{AB}=0\,\,\,\,\,\,\,\,\,\mathrm{(d)}\,\,\,\vec{v}^{\, E}_{02}=\vec{v}^{\, E}_{01}
  2. ¿Dónde se halla el centro instantáneo de rotación I_{20}\,\,?
    \mathrm{(a)}\,\,\,I_{20}\equiv C\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(b)}\,\,\,I_{20}\equiv H\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(c)}\,\,\,I_{20}\equiv G\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(d)}\,\,\,I_{20}\equiv F

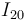2 Solución

El disco "0" rueda sin deslizar sobre el eje OX\, de la escuadra "1". La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {01} coincide con el punto de contacto entre dicho disco y dicho eje:

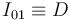
I_{01}\equiv D

Entonces, aplicando la ley de composición de velocidades en el punto D\,, se obtiene:

\vec{v}^{\, D}_{21}=\vec{v}^{\, D}_{20}+\underbrace{\vec{v}^{\, D}_{01}}_{\displaystyle\vec{0}}\,\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{v}^{\, D}_{21}=\vec{v}^{\, D}_{20}

resultando ser VERDADERA la igualdad (a) de la primera pregunta.

Por otra parte, el disco "2" rueda sin deslizar sobre el eje OY\, de la escuadra "1". La ausencia de deslizamiento implica que el centro instantáneo de rotación del movimiento {21} coincide con el punto de contacto entre dicho disco y dicho eje:

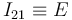
I_{21}\equiv E

Entonces, aplicando la ley de composición de velocidades en el punto 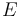E\,, se obtiene:

\vec{v}^{\, E}_{01}=\vec{v}^{\, E}_{02}+\,\,\underbrace{\vec{v}^{\, E}_{21}}_{\displaystyle\vec{0}}\,\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{v}^{\, E}_{02}=\vec{v}^{\, E}_{01}

resultando ser VERDADERA la igualdad (d) de la primera pregunta.

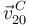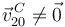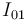En cuanto al movimiento {20}, se sabe que el disco "2" se mantiene siempre en contacto tangente con el disco "0". Al ser C\, el punto de contacto entre ambos discos, la velocidad \vec{v}^{\, C}_{20}\, es la velocidad de deslizamiento entre ambos sólidos (sabemos que \vec{v}^{\, C}_{20}\neq\vec{0}\, porque C\, no está alineado con I_{21}\, e I_{01}\, y, por tanto, según el teorema de los tres centros I_{20}\not\equiv C\,). Pero la velocidad de deslizamiento entre dos sólidos en contacto puntual es siempre tangencial al contacto (si no fuera así, perderían el contacto). Entonces podemos asegurar que:

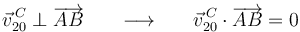
\vec{v}^{\, C}_{20}\perp \overrightarrow{AB}\,\,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{v}^{\, C}_{20}\cdot\overrightarrow{AB}=0

resultando ser VERDADERA la igualdad (C) de la primera pregunta.

En cuanto a la primera pregunta, habiéndose visto ya que son verdaderas las igualdades (a), (c) y (d), sólo falta comprobar que la igualdad falsa (la que hay que marcar) es la igualdad (b).

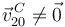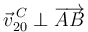En efecto, teniendo en cuenta que \vec{v}^{\, C}_{20}\neq\vec{0}\, y que \vec{v}^{\, C}_{20}\perp \overrightarrow{AB}\,, llegamos a la conclusión de que:

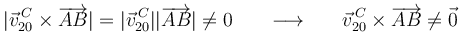
|\vec{v}^{\, C}_{20}\times\overrightarrow{AB}|=|\vec{v}^{\, C}_{20}||\overrightarrow{AB}|\neq 0\,\,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{v}^{\, C}_{20}\times\overrightarrow{AB}\neq\vec{0}

resultando ser FALSA la igualdad (b) de la primera pregunta.

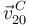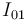Por último, trazando la perpendicular a \vec{v}^{\, C}_{20}\, en el punto C\, y trazando la recta que pasa por los puntos I_{21}\, e I_{01}\, (en aplicación del teorema de los tres centros), hallaremos el punto 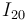I_{20}\, en la intersección de ambas rectas:

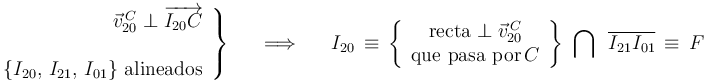
\left.\begin{array}{r} \vec{v}_{20}^{\, C}\perp\overrightarrow{I_{20}C} \\ \\ \{I_{20},\, I_{21},\,I_{01} \} \,\,\mathrm{alineados} \end{array}\right\} \,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\, I_{20}\,\equiv\,\left\{\begin{array}{c} \mathrm{recta}\perp\vec{v}_{20}^{\, C} \\ \mathrm{que}\,\,\mathrm{pasa}\,\,\mathrm{por} \, C \end{array}\right\}\,\,\bigcap\,\,\,\overline{I_{21}I_{01}}\,\equiv\,F

Así que la respuesta correcta a la segunda pregunta es la (d) 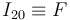\,\,\,I_{20}\equiv F\,.

Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Dos_discos_III_(Ex.Ene/20)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace