No Boletín - Altura de un triángulo (Ex.Oct/19)
De Laplace
Revisión a fecha de 18:17 11 feb 2020; Enrique (Discusión | contribuciones)
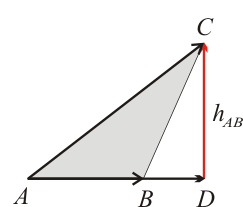
1 Enunciado
Sea un triángulo 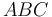 arbitrario. Denominamos
arbitrario. Denominamos 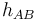 a la longitud de su altura respecto del lado
a la longitud de su altura respecto del lado  . ¿Cuál de las siguientes igualdades es correcta?
. ¿Cuál de las siguientes igualdades es correcta?
(NOTA: sólo una de las cuatro opciones es correcta).
- (1)
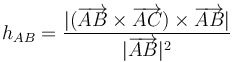
- (2)
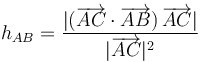
- (3)
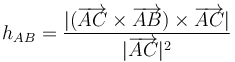
- (4)
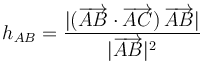
2 Solución
Utilizando una fórmula deducida en la teoría, descomponemos el vector 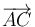 en la suma de un vector paralelo a
en la suma de un vector paralelo a 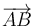 (vector
(vector 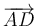 ) y un vector perpendicular a
) y un vector perpendicular a 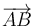 (vector
(vector  ):
):

Resulta obvio que la longitud de la altura buscada coincide precisamente con el módulo del vector perpendicular a 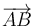 de la citada descomposición, es decir:
de la citada descomposición, es decir:
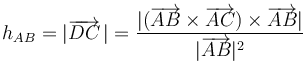
Así que la solución correcta es la (1).