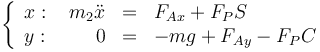Anilla ensartada en un aro rodante
De Laplace
Contenido |
1 Enunciado
Se tiene un sistema formado por un aro “2” de masa m2 que puede rodar sin deslizar sobre una superficie horizontal “1”. Ensartado en este aro se encuentra una pequeña anilla “3” de masa m3 que puede deslizarse sin fricción a lo largo del aro “2”.
Empleando como coordenadas la posición x del centro C del aro “2” a lo largo del eje horizontal y el ángulo θ que la posición de la anilla “3” forma con la vertical, determine:
- Las ecuaciones de movimiento para estas dos coordenadas.
- Dos constantes de movimiento no triviales.
- Suponiendo que el aro y la anilla están en reposo, se sitúa la anilla formando un pequeño ángulo θ0 con la vertical. Determine la frecuencia de las oscilaciones que realiza el sistema.
2 Ecuaciones de movimiento
Cada uno de los dos cuerpos “2” y “3” obedece las ecuaciones dadas por el teorema de la cantidad de movimiento y el teorema del momento cinético. En cada caso debemos incluir las posibles fuerzas de reacción sobre cada uno de los cuerpos.
2.1 Para el aro
2.1.1 Teorema de la cantidad de movimiento
El aro experimenta las siguientes fuerzas externas:
- Su peso
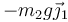
- La reacción del suelo en el punto de contacto A, la cual tiene dos componentes
- Una vertical
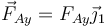 que impide que el aro atraviese el suelo, y mantiene el centro a una altura constante R.
que impide que el aro atraviese el suelo, y mantiene el centro a una altura constante R.
- Una horizontal,
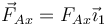 que impide que el aro deslice, de manera que solo ruede.
que impide que el aro deslice, de manera que solo ruede.
- Una vertical
- Una fuerza de reacción debida a la anilla. El vínculo de que la anilla permanezca en el aro se consigue realizando una fuerza normal sobre ésta
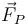 y, por la tercera ley de Newton, una fuerza igual y de sentido contrario
y, por la tercera ley de Newton, una fuerza igual y de sentido contrario 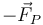 se aplica en el aro.
se aplica en el aro.
Esto nos da la sigueinte relación
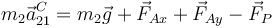
La aceleración del centro del aro es puramente horizontal
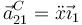
Para expresar la fuerza 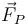 usamos un sistema “3” de ejes que está girado un ángulo θ respecto al sistema “1”, de manera que
usamos un sistema “3” de ejes que está girado un ángulo θ respecto al sistema “1”, de manera que 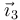 es tangente al aro y
es tangente al aro y 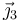 es radial y hacia adentro.
es radial y hacia adentro.

( ). Estos vectores se relacionan directamente con los correspondientes a las coordenadas polares.
). Estos vectores se relacionan directamente con los correspondientes a las coordenadas polares.
Tenemos entonces
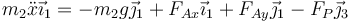
Separando por componentes