Problemas de dinámica del sólido rígido (GIOI)

De Laplace

1 Momento de inercia de un sistema de partículas

Se tiene un sólido formado por ocho partículas de masa m situadas en los vértices de un cubo de arista b.

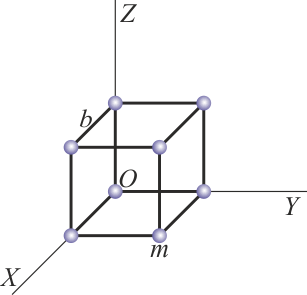
Halle el momento de inercia del cubo respecto a los siguientes ejes:

1. Uno perpendicular a una cara y que pase por el centro del cubo.
2. Uno que pase por dos vértices opuestos.
3. Uno que pase por los centros de dos aristas opuestas.
4. Uno que pase por una arista

Solución

2 Momento de inercia de sólidos esféricos

Calcule el momento de inercia de una esfera maciza, de masa M y radio R alrededor de de un eje que pasa por su centro.

A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa M, radio interior R₁ y exterior R₂ respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio R?

Solución

3 Momento de inercia de sólidos cilíndricos

Halle los siguientes momentos de inercia de sólidos de densidad homogénea:

1. Una superficie cilíndrica hueca, de masa M, radio R y altura H.
2. Un cilindro macizo, de masa M, radio R y altura H.
3. Una corona cilíndrica de masa M, radio interior R₁ y exterior R₂, con altura H

En todos los casos, el momento de inercia debe hallarse respecto al eje del cilindro.

Solución

4 Barra sujeta por un cable

Una mesa plegable está articulada a la pared por un extremo, y cuelga de la pared por un cable tirante. En dos dimensiones esto se puede modelar como una barra de longitud b y masa m distribuida uniformemente. La barra está articulada por su extremo A y atada por su extremo B a una pared vertical, de forma que el cable forma un ángulo de 45° con la vertical.

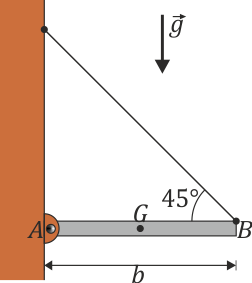
Calcule la tensión del cable, así como la fuerza de reacción en el punto A.

Solución