Problemas de energía y leyes de conservación (GIOI)

De Laplace

1 Conservación en un movimiento rectilíneo y uniforme

Una partícula de masa m describe el movimiento rectilíneo y uniforme

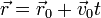
Demuestre que su cantidad de movimiento, su momento cinético respecto al origen de coordenadas y su energía cinética permanecen constantes. Halle el valor de estas tres cantidades.

Solución

2 Leyes de conservación en polares y cilíndricas

Una partícula de masa m describe el movimiento expresado en cilíndricas

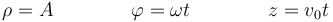
Determine si se conserva la cantidad de movimiento, el momento cinético respecto al origen de coordenadas y la energía cinética. En su caso, halle el valor de las constantes.

Solución

3 Trabajo en una semicircunferencia

Calcule el trabajo realizado por la gravedad cuando una partícula de masa m que pasa de estar a una altura 2R a estar al nivel del suelo (a) si el movimiento es una recta vertical (b) Desciende a lo largo de una semicircunferencia de radio R.

Solución

4 Trabajo por rozamiento

Calcule igualmente el trabajo realizado por la fuerza de rozamiento seco sobre una masa m que se hace deslizar por una mesa horizontal con la cual tiene un coeficiente de rozamiento μ, si (a) el movimiento es a largo de un segmento de longitud 2R, (b) el deslizamiento es a largo de una semicircunferencia de radio R.

Solución

5 Conservación en un oscilador armónico tridimensional

Una partícula de masa 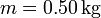se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke

siendo su posición y velocidad iniciales

1. Calcule el momento cinético de la partícula respecto al origen de coordenadas
2. Halle la energía mecánica de la partícula
3. Determine las distancias máxima y mínima a las que pasa del origen, así como la rapidez mínima que alcanza

Solución

6 Rapidez y tensión de un péndulo

Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo simple de masa m y longitud L pasa por su punto más bajo, como función del ángulo máximo θ₀ con el que se separa de la vertical.

Compare este resultado con el que se obtiene empleando la aproximación lineal. Determine el error relativo cometido con esta aproximación para , ,…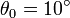

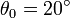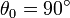
Determine la tensión de la cuerda en el punto más bajo y en el punto de máxima separación de la vertical. en función del ángulo θ₀

Solución

7 Energía en el salto desde un puente

Haciendo puenting (bungee jumping en inglés), Alberto, de 75 kg, se deja caer desde el pretil de un puente situado a 70 m de altura sobre un río empleando una cuerda elástica de 30 m.

1. Determine la constante elástica k que debe tener la cuerda para que Alberto llegue a rozar el agua del río.
2. Si, empleando la misma goma, se deja caer Benito, de 90 kg, ¿con qué rapidez impactará con el agua? ¿Cuánta cuerda debería recoger si quiere llegar él también rozando al agua?

Solución

8 Anilla ensartada en un aro

Se tiene un aro circular de radio R situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa m situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:

1. Una anilla ensartada en el aro
2. Una bolita que desliza por el interior del aro, sin estar unida a él.

Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.

Solución

9 Partícula que se despega de esfera

Una partícula de masa m se encuentra en lo alto de una cúpula hemisférica de radio R, sobre la cual la masa puede deslizar sin rozamiento. La semiesfera está rígidamente unida a una superficie horizontal. La masa está sometida a la acción del peso. Estando en esta posición se le comunica una velocidad horizontal de rapidez v₀

1. Supóngase en primer lugar que v₀ = 0
   1. Determine el punto de la esfera en el que la partícula se despega de ella.
   2. ¿Qué rapidez tiene la partícula en el momento en que impacta con el suelo?
2. Supongamos ahora una cierta rapidez inicial v₀.
   1. Determine el punto en el que la masa despega de la superficie esférica, dando el ángulo θ que el vector de posición relativa al centro de la esfera forma con la vertical.
   2. ¿Cuál es el valor mínimo de v₀ para que la partícula despegue directamente de la superficie, sin deslizar sobre ella?
   3. Para este valor mínimo de v₀ determine la distancia al centro de la semiesfera del punto de la superficie horizontal en el que impacta la partícula.

Solución