Problemas de energía y leyes de conservación (GIOI)

De Laplace

Revisión a fecha de 20:30 2 ene 2006; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Conservación en un movimiento rectilíneo y uniforme
2 Leyes de conservación en polares y cilíndricas
3 Trabajo en una semicircunferencia
4 Trabajo por rozamiento
5 Conservación en un oscilador armónico tridimensional
6 Rapidez y tensión de un péndulo

1 Conservación en un movimiento rectilíneo y uniforme

Una partícula de masa $m$ describe el movimiento rectilíneo y uniforme

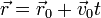
$\vec{r}=\vec{r}_0+\vec{v}_0t$

Demuestre que su cantidad de movimiento, su momento cinético respecto al origen de coordenadas y su energía cinética permanecen constantes. Halle el valor de estas tres cantidades.

Solución

2 Leyes de conservación en polares y cilíndricas

Una partícula de masa $m$ describe el movimiento expresado en cilíndricas

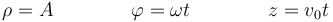
$\rho = A\qquad\qquad \varphi = \omega t\qquad\qquad z = v_0t$

Determine si se conserva la cantidad de movimiento, el momento cinético respecto al origen de coordenadas y la energía cinética. En su caso, halle el valor de las constantes.

Solución

3 Trabajo en una semicircunferencia

Calcule el trabajo realizado por la gravedad cuando una partícula de masa $m$ que pasa de estar a una altura $2 R$ a estar al nivel del suelo (a) si el movimiento es una recta vertical (b) Desciende a lo largo de una semicircunferencia de radio $R$ .

Solución

4 Trabajo por rozamiento

Calcule igualmente el trabajo realizado por la fuerza de rozamiento seco sobre una masa $m$ que se hace deslizar por una mesa horizontal con la cual tiene un coeficiente de rozamiento $μ$ , si (a) el movimiento es a largo de un segmento de longitud $2 R$ , (b) el deslizamiento es a largo de una semicircunferencia de radio $R$ .

Solución

5 Conservación en un oscilador armónico tridimensional

Una partícula de masa 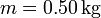$m=0.50\,\mathrm{kg}$ se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke

$\vec{F}=-k\vec{r}\qquad\qquad k = 2.00\,\mathrm{N}/\mathrm{m}$

siendo su posición y velocidad iniciales

$\vec{r}_0 = (-12.0\,\vec{\imath}+11.0\vec{\jmath})\,\mathrm{m}\qquad \qquad \vec{v}_0=(-8.0\vec{\imath}+24.0\,\vec{\jmath})\,\frac{\mathrm{m}}{\mathrm{s}}$

Calcule el momento cinético de la partícula respecto al origen de coordenadas
Halle la energía mecánica de la partícula
Determine las distancias máxima y mínima a las que pasa del origen, así como la rapidez mínima que alcanza

Solución

6 Rapidez y tensión de un péndulo

Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo simple de masa $m$ y longitud $L$ pasa por su punto más bajo, como función del ángulo máximo $θ 0$ con el que se separa de la vertical.

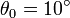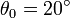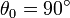
Compare este resultado con el que se obtiene empleando la aproximación lineal. Determine el error relativo cometido con esta aproximación para $\theta_0=10^\circ$ , $\theta_0=20^\circ$ ,… $\theta_0=90^\circ$