Segunda Convocatoria Ordinaria 2017/18 (G.I.E.R.M.)

De Laplace

Revisión a fecha de 18:20 15 ene 2019; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Dos partículas unidas por una barra

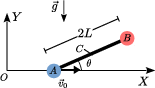
Las partículas $A$ y $B$ , ambas con masa $m$ , están unidas por una barra rígida de longitud $2 L$ y masa despreciable. El punto $C$ es el punto medio de la barra. La partícula $A$ está obligada a moverse en el eje fijo $O X$ , como se indica en la figura. Este contacto es liso. La barra que une las partículas forma un ángulo $θ(t)$ con el eje $O X$ . La partícula $A$ se mueve con velocidad constante 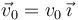$\vec{v}_0 = v_0\,\vec{\imath}$ . En el instante inicial la partícula $A$ se encontraba en el punto $O$ y $θ(0) = 0$ . El sistema está sometido a la acción de la gravedad.

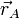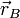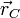Encuentra la expresión de los vectores de posición $\vec{r}_A$ , $\vec{r}_B$ y $\vec{r}_C$ en función de $v 0$ , $L$ , $θ$ y $t$ .
Si el ángulo varía como 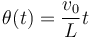$\theta(t)=\dfrac{v_0}{L}t$ , calcula la velocidad y aceleración de las partículas $A$ y $B$ y del centro de masas del sistema.
El movimiento descrito anteriormente está producido por una fuerza horizontal 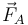$\vec{F}_A$ aplicada sobre la partícula $A$ . Dibuja el diagrama de fuerzas del sistema y calcula la expresión de todas las fuerzas externas que actúan sobre él.
Calcula la energía cinética del sistema y su momento cinético respecto de $O$ en el instante $t 1 = π L / 2 v 0$ .
Supongamos ahora que la partícula $B$ se mueve de modo que la componente de su velocidad sobre el $O X$ es constante e igual a $2 v 0$ . Encuentra y resuelve la ecuación diferencial que debe cumplir $θ(t)$ para que esto sea posible.

2 Barra girando alrededor de otra barra horizontal

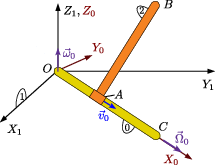
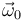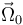Una barra de longitud $L$ (sólido "0") puede rotar alrededor del eje $O Z 1$ con velocidad angular constante $\vec{\omega}_0$ , como se indica en la figura. El punto $O$ de la barra es fijo. La barra "0" siempre está contenida en el plano $O X 1 Y 1$ . Otra barra, también de longitud $L$ (sólido "2"), está conectada a la barra "0" por un pasador en el punto $A$ . El pasador desliza sobre la barra "0" con velocidad constante $v 0$ . 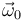Además, la barra "2" gira alrededor de la barra "0" con velocidad angular uniforme $\vec{\Omega}_0$ . En $t = 0$ la barra "0" estaba sobre el eje $O X 1 +$ , el extremo $A$ de la barra "2" estaba en el punto $O$ y el punto $B$ estaba en el plano $O X 1 Y 1$ . 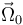Los vectores $\vec{v}_0$ , $\vec{\omega}_0$ y $\vec{\Omega}_0$ apuntan en el sentido indicado en la figura.

Determina las reducciones cinemáticas ${01},{20},{21}$ .
Calcula las derivadas temporales de las reducciones cinemáticas del apartado anterior.
¿Qué tipo de movimiento es cada uno de ellos?
Sea $t 1$ el instante de tiempo para el cual $B$ está en el punto más alto de su trayectoria. Calcula 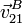$\vec{v}^{B}_{21}$ y $\vec{a}^B_{21}$ en ese instante.

Segunda Convocatoria Ordinaria 2017/18 (G.I.E.R.M.)

De Laplace

1 Dos partículas unidas por una barra

2 Barra girando alrededor de otra barra horizontal

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES