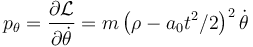Test de la 2ª convocatoria CMR 2017-2018
De Laplace
Contenido |
1 Sistema de partículas
En un sistema de partículas sometidas exclusivamente a fuerzas internas newtonianas, ¿cuál de las siguientes cantidades no es una constante de movimiento, en general?
- A La cantidad de movimiento del sistema.
- B El momento cinético respecto al centro de masas del sistema.
- C El momento cinético respecto a un punto fijo O.
- D La energía mecánica del sistema.
- Solución
La respuesta correcta es la D.
Las leyes para un sistema de partículas son
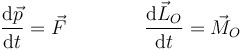
con 
la resultante de las fuerzas externas y 
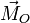el moemnto resultante de las fuerzas externas (O es un punto fijo o el CM). Si no hay fuerzas externas, 
, 
y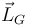 
.
La energía mecánica, en cambio, si puede verse afectada por fuerzas internas. Por ejemplo, el rozamiento entre piezas de un mecanismo frena estos.
2 Oscilador sobreamortiguado
Un oscilador armónico sobreamortiguado tiene la masa inicialmente en la posición de equilibrio. En ese momento se le comunica una velocidad inicial v_0. ¿Cómo es el movimiento de la masa?
- A Inicialmente se aleja hasta una distancia máxima y luego retorna a la posición inicial de forma más lenta que si el amortiguador fuera crítico.
- B Se va alejando cada vez más lentamente hasta detenerse (tras un tiempo infinito) a una cierta distancia de la posición inicial.
- C Describe un movimiento oscilatorio en el que la amplitud va decayendo exponencialmente con el tiempo.
- D Inicialmente se aleja hasta una distancia máxima y luego retorna a la posición inicial de forma más rápida que si el amortiguador fuera crítico.
- Solución
La respuesta correcta es la A.
Tal como se ve en teoría el comportamiento de un oscilador sobreamortiguado es de la forma
3 Sistema de fuerzas
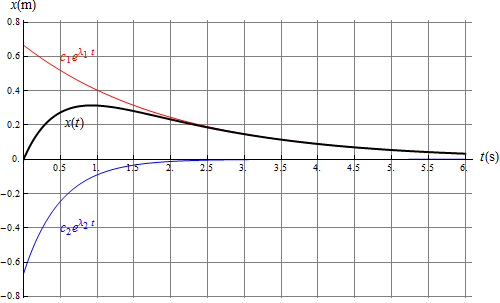
Sobre un sólido actúan simultáneamente tres fuerzas: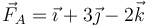 
aplicada en A(2,1,0), 
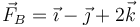aplicada en B(1,0,0) y 
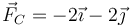aplicada en C(0,-2,1) (fuerzas en N, posiciones en m). ¿A qué se reduce este sistema de fuerzas?
- A Es un sistema nulo.
- B Un par de fuerzas.
- C Una fuerza única.
- D Un tornillo.
- Solución
La respuesta correcta es la A.
No hay más que calcular la resultante
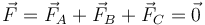
y el momento resultante
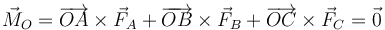
4 Rotación de un sólido
Un sólido rígido describe un movimiento tal que en un instante dado su velocidad angular es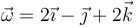 
(rad/s) y la velocidad del punto A(2,1,2) (m) es 
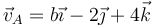(m/s).
4.1 Pregunta 1
¿Cuánto debe valer la cantidad b si se sabe que el movimiento instantáneo es de rotación?
- A 4 m/s.
- B −5 m/s.
- C −3 m/s.
- D no hay suficiente información para saberlo.
- Solución
La respuesta correcta es la B.
La velocidad de cada punto debe ser ortogonal a la velocidad angular
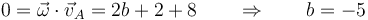
4.2 Pregunta 2
Para el movimiento anterior, ¿Cuál de los siguientes puntos pertenece al EIR?
- A B(2,-1,1)
- B C(1,3,-1)
- C O(0,0,0)
- D D(4,-2,-3)
- Solución
La respuesta correcta es la A.
En una rotación los puntos del eje cumplen
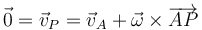
Probando con los distintos puntos, a la primera sale que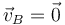 
.
5 Juntas acopladas
Se tiene una unión formada por dos juntas Cardán de dos ejes puestas consecutivamente. ¿Cuántos grados de libertad tiene el último sólido respecto al primero?
- A 2.
- B 3.
- C 4.
- D 6.
- Solución
La respuesta correcta es la C.
Una junta Cardán de dos ejes tiene dos grados de libertad. Una sucesión de dos juntas tiene 2×2 = 4 grados de libertad. Bloqueando una de ellas se consiguen dos rotaciones y moviéndolas a la vez resultan dos traslaciones.
6 Desplazamientos virtuales
Una partícula está ensartada en una varilla horizontal que pasa por el origen de coordenadas. Esta varilla gira con velocidad angular Ω constante alrededor del origen. Si (x,y) son las coordenadas de la partícula, ¿qué vinculo cumplen los desplazamientos virtuales de estas coordenadas (aquí S = sen(Ωt), C = cos(Ωt)?
- A 2. -xS+yC=0
- B 2.-S dx+C dy-Ω(xC+yS) dt=0
- C 2.-S δx+C δy=0
- D 2.-S δx+C δy-Ω(xC+yS) δt=0
- Solución
La respuesta correcta es la C.
Los desplazamientos virtuales cumplen la ecuación del vínculo supuesto éste congelado en el tiempo. En la práctica, ello implica una relación entre diferenciales en la que no aparece el término en dt o δt. Solo la opción C cumple esto.
7 Constante de movimiento
La lagrangiana de un sistema tiene la forma, en unidades adecuadas
¿Cuál de las siguientes cantidades es una constante de movimiento (o integral primera) de este sistema?
- A
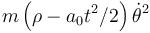
- B
̇
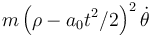- C No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): m\left(\left(\rho_a_0t\right)^2+\left(\rho-a_0t^2/2\right)\dot{\theta}^2\right)/2-k\rho^2/{2}
- A
- D No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): m\left(\left(\rho_a_0t\right)^2+\left(\rho-a_0t^2/2\right)\dot{\theta}^2\right)/2+k\rho^2/{2}
- Solución
La respuesta correcta es la B.
La energía no se conserva porque la lagrangiana depende del tiempo.
La coordenada θ es cíclica (no aparece en la lagrangiana), por tanto su momento conjugado es una constante de movimiento.
