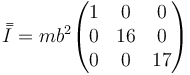Sistema de dos masas unidas por una varilla (CMR)

De Laplace

Revisión a fecha de 20:25 18 ago 2018; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Centro de masas
3 Tensor de inercia
- 3.1 Respecto al eje OX
- 3.2 Respecto al eje OY
4 =Respecto al eje OZ
- 4.1 Productos de inercia
- 4.2 Forma matricial
5 Ejes y momentos principales
6 Momento y energía cinética
7 Fuerza y par

1 Enunciado

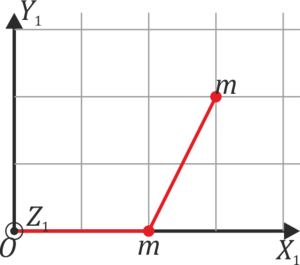
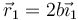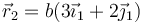Un sólido está formado por dos masas iguales, $m 1 = m 2 = m$ , unidas por una varilla sin masa. En un instante dado, las dos partículas se hallan en $\vec{r}_1=2b\vec{\imath}_1$ y $\vec{r}_2=b(3\vec{\imath}_1+2\vec{\jmath}_1 )$ , respectivamente.

¿Cuál es la posición del CM del sistema?
¿Cuánto vale su tensor de inercia respecto al triedro $O X 1 Y 1 Z 1$ ?
Determine los ejes principales de inercia y los momentos principales de inercia de este sólido.
Si la varilla gira con velocidad angular constante 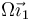$\Omega\vec{\imath}_1$ alrededor del eje $O X 1$ , ¿cuánto vale su momento cinético respecto a O? ¿Y su energía cinética?
Para el movimiento anterior, ¿qué fuerza y que momento hay que aplicar en O para mantener el sistema en movimiento?

2 Centro de masas

Al ser las dos masas iguales, el centro de masas se halla en el punto medio

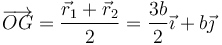
$\overrightarrow{OG}=\frac{\vec{r}_1+\vec{r}_2}{2}=\frac{3b}{2}\vec{\imath}+b\vec{\jmath}$

3 Tensor de inercia

Para un sistema de masas puntuales, basta con sumar las contribuciones de cada una a los diferentes momentos y productos de inercia.

3.1 Respecto al eje OX

La masa 1 se halla sobre el propio eje y la 2 a una distancia 2b, por tanto

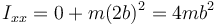
$I_{xx}=0+m(2b)^2=4mb^2\,$

3.2 Respecto al eje OY

La masa 1 está a 2b y la 2 a 3b

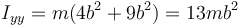
$I_{yy}=m(4b^2+9b^2)=13mb^2\,$

4 =Respecto al eje OZ

Se trata de una figura plana en el plano $O X 1 Y 1$ por lo que

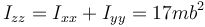
$I_{zz}=I_{xx}+I_{yy}=17mb^2\,$

4.1 Productos de inercia

Por ser una figura plana en $O X 1 Y 1$

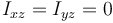
$I_{xz}=I_{yz}=0\,$

El único elemento no diagonal no nulo es el xy

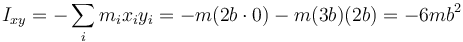
$I_{xy}=-\sum_i m_i x_iy_i=-m(2b\cdot 0)-m(3b)(2b)=-6mb^2\,$

4.2 Forma matricial

Reuniendo los resultados anteriores queda la matriz

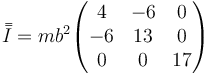
$\bar{\bar{I}}=mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17\end{pmatrix}$

También se puede calcular esta matriz directamente en lugar de elemento a elemento, partiendo de la expresión

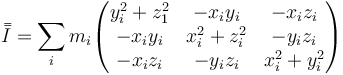
$\bar{\bar{I}}=\sum_i m_i\begin{pmatrix} y_i^2+z_1^2 & -x_iy_i & -x_iz_i \\ -x_iy_i & x_i^2+z_i^2 & -y_iz_i \\ -x_iz_i & -y_iz_i & x_i^2+y_i^2 \end{pmatrix}$

que en este caso nos da

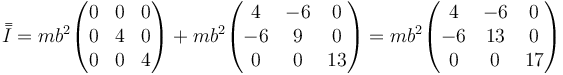
$\bar{\bar{I}}=mb^2\begin{pmatrix} 0 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 4 \end{pmatrix}+mb^2\begin{pmatrix} 4 & -6 & 0 \\ -6 & 9 & 0 \\ 0 & 0 & 13 \end{pmatrix}=mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17\end{pmatrix}$

5 Ejes y momentos principales

los momentos principales de inercia resultan de resolver el determinante

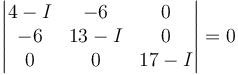
$\left|\begin{matrix}4-I & -6 & 0 \\ -6 & 13-I & 0 \\ 0 & 0 & 17-I \end{matrix}\right|=0$

(donde en elr esultado final habrá que multiplicar el número que salga por $m b 2$ ). Desarrollamos el determinante

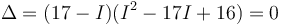
$\Delta = (17-I)(I^2-17I+16)=0\,$

Uno de los autovalores es inmediato, $I Z Z = 17 m b 2$ . Esto era de esperar pues ya sabíamos que el eje OZ era principal. Los otros dos salen de una ecuación de segundo grado

$I_{XX}=mb^2 \qquad\qquad I_{YY}=16mb^2$

Para hallar cada autovector resolvemos la ecuación vectorial. Para I_{ZZ} es inmediato

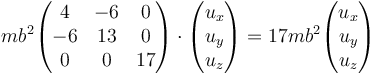
$mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17 \end{pmatrix}\cdot\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}=17mb^2\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}$

que da el sistema

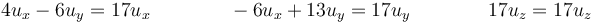
$4u_x-6u_y=17u_x\qquad\qquad -6u_x+13u_y=17u_y \qquad\qquad 17u_z=17u_z$

con solución

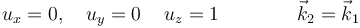
$u_x=0,\quad u_y=0\,\quad u_z=1\qquad\qquad\vec{k}_2=\vec{k}_1$

Para el autovalor $I X X$ operamos de la misma forma

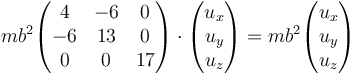
$mb^2\begin{pmatrix}4 & -6 & 0 \\ -6 & 13 & 0 \\ 0 & 0 & 17 \end{pmatrix}\cdot\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}=mb^2\begin{pmatrix}u_x \\u_y\\ u_z\end{pmatrix}$

que da el sistema

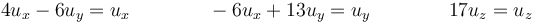
$4u_x-6u_y=u_x\qquad\qquad -6u_x+13u_y=u_y \qquad\qquad 17u_z=u_z$

con solución

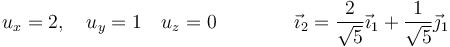
$u_x=2,\quad u_y=1\quad u_z=0\qquad\qquad\vec{\imath}_2=\frac{2}{\sqrt{5}}\vec{\imath}_1+\frac{1}{\sqrt{5}}\vec{\jmath}_1$

donde en el última paso se ha normalizado el vector.

Por último, para el autovalor $I Y Y = 16 m b 2$ resulta el tercer vector del triedro

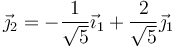
$\vec{\jmath}_2=-\frac{1}{\sqrt{5}}\vec{\imath}_1+\frac{2}{\sqrt{5}}\vec{\jmath}_1$

En esta base, el tensor de inercia se escribe

$\bar{\bar{I}}=mb^2\begin{pmatrix}1 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 17 \end{pmatrix}$

6 Momento y energía cinética

7 Fuerza y par

Sistema de dos masas unidas por una varilla (CMR)

De Laplace

Contenido

1 Enunciado

2 Centro de masas

3 Tensor de inercia

3.1 Respecto al eje OX

3.2 Respecto al eje OY

4 =Respecto al eje OZ

4.1 Productos de inercia

4.2 Forma matricial

5 Ejes y momentos principales

6 Momento y energía cinética

7 Fuerza y par

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES