Ecuación para las ondas en una cuerda tensa
De Laplace
Contenido |
1 Objetivo
Al principio de este tema se estudia la ecuación de onda en su forma matemática, pero para que esa ecuación sea útil, hay que demostrar que aparece realmente en situaciones físicas.
En esta sección vamos a probar que las ondas que se transmiten por una cuerda tensa verifican, en condiciones adecuadas, la ecuación de onda unidimensional.
Suponemos que tenemos una cuerda de gran longitud L, de sección uniforme S y con una densidad de masa por unidad de longitud μ (que será igual a su densidad de masa por unidad de volumen, ρ, multiplicada por la sección de la cuerda μ = ρS).
Esta cuerda está sometida a tensión, por ejemplo, atando uno de sus extremos a una pared y colgando un peso del otro extremo.
Por efecto de las perturbaciones esta cuerda vibra transversalmente, de forma que un punto de ella, de coordenada x se desplaza una cantidad y en la dirección perpendicular a la cuerda.
Supondremos que las deformaciones son de pequeña amplitud, de forma que puede suponerse que la longitud de la cuerda no se ve afectada por la curvatura, y que cada punto de la cuerda se mueve solo transversalmente y no hacia adelante o hacia atrás.
2 Dinámica de un elemento de cuerda
Consideremos un trozo de cuerda de longitud infinitesimal, comprendido entre las posiciones x y x + Δx. Este trozo tendrá una masa muy pequeña
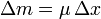
Esta masa puede tratarse como una partícula que se mueve exclusivamente en la dirección vertical, según hemos supuesto, de forma que la velocidad y aceleración de esta masa es
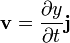
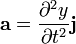
El uso de la derivada parcial, en vez de la total, indicada normalmente con uno (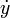 ) o dos puntos (
) o dos puntos (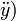 sobre la variable, se debe a que y depende realmente de dos variables, x y t. La velocidad y la aceleración correspondientes a un movimiento vertical (variación en t) sin que se modifique la posición horizontal (x constante). Esta es justamente la definición de derivada parcial.
sobre la variable, se debe a que y depende realmente de dos variables, x y t. La velocidad y la aceleración correspondientes a un movimiento vertical (variación en t) sin que se modifique la posición horizontal (x constante). Esta es justamente la definición de derivada parcial.
Este trozo infinitesimal de cuerda se mueve sometida a la acción de las fuerzas ejercidas por los trozos de cuerda adyacentes, a través de la tensión 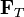 con que tiran de ella. De esta forma, la segunda ley de Newton para esta masa puntual se escribirá
con que tiran de ella. De esta forma, la segunda ley de Newton para esta masa puntual se escribirá
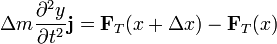
El signo menos en la segunda tensión se debe a que consideramos la tensión siempre como la que el elemento situado en x + Δx tira del elemento anterior, situado en x. Si consideramos la fuerza con la que un elemento tira del siguiente, en vez del anterior, habrá que cambiarle el signo.
Veamos cada componente de esta ecuación vectorial por separado.
3 Componente longitudinal
Si consideramos la dirección longitudinal, paralela a la cuerda, tenemos que en esta dirección la aceleración es nula (pues la onda es transversal), así que la segunda ley de Newton se reduce a
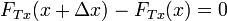
Siendo FTx las componentes de la tensión (que, como toda fuerza, es un vector) en la dirección longitudinal. Podemos relacionar estas componentes con el módulo de la tensión, 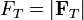 , y el ángulo θ que forma con la dirección lomgitudinal
, y el ángulo θ que forma con la dirección lomgitudinal
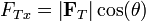
con lo que nos queda
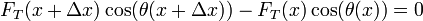
Ahora bien, por ser pequeña la amplitud de las oscilaciones, este ángulo \theta es siempre muy pequeño, de forma que podemos hacer la aproximación
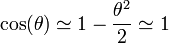
de forma que la ecuación de movimiento en la dirección longitudinal se reduce a
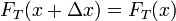
o, lo que es lo mismo, la tensión es la misma, en módulo, para todos los puntos de la cuerda. Por ello se puede hablar de la ”tensión de la cuerda“ sin especificar a qué punto nos referimos. Hay que recordar, no obstante, que este resultado es aproximado, consecuencia de haber supuesto pequeñas amplitudes.
4 Componente transversal
En la dirección transversal sí debemos considerar la aceleración del elemento de masa, de forma que nos queda
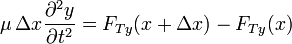
Relacionando de nuevo las componentes con el módulo (del cual ya sabemos que es constante) y el ángulo nos queda
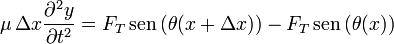
Aplicando de nuevo que el ángulo es pequeño, podemos hacer una doble aproximación
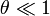

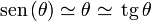
(recordemos que el coseno vale prácticamente la unidad). Esto nos convierte la ecuación para la componente transversal en
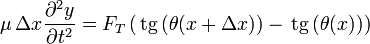
Ahora bien, la tangente del ángulo θ es justamente la pendiente de la recta tangente a la curva, esto es, la derivada con respecto a x
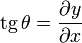
así que la ecuación anterior la podemos escribir como (pasando Δx al segundo miembro)
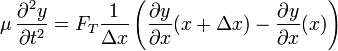
pero, para una función cualquiera en un instante dado
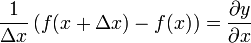
así que nos queda finalmente
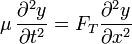
que es la ecuación de onda que buscábamos.





