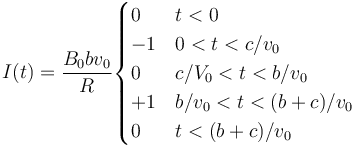Espira que entra en una franja campo magnético (GIE)

De Laplace

Revisión a fecha de 21:10 20 jun 2018; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Intensidad de corriente
3 Potencia disipada
4 Fuerza sobre la espira
5 Potencia mecánica
6 Energía total disipada

1 Enunciado

Una espira cuadrada de lado $b$ y resistencia eléctrica $R$ se encuentra en el plano $z = 0$ con lados paralelos a los ejes. La espira se halla inmersa en un campo magnético dependiente de la posición como

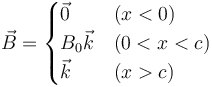
$\vec{B}=\begin{cases}\vec{0} & (x<0) \\ B_0\vec{k} & (0<x<c) \\ \vec{k} & (x>c)\end{cases}$

siendo $c$ una constante que cumple $c < b$ . La espira es obligada a moverse con velocidad constante 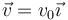$\vec{v}=v_0\vec{\imath}$ . En $t = 0$ el lado delantero de la espira se halla en $x = 0$ . Determine, como función del tiempo:

La intensidad de corriente inducida en la espira.
La potencia disipada por efecto Joule.
La fuerza magnética sobre la espira.
La potencia mecánica sobre la espira debida al agente que mantiene la espira con velocidad constante.
Calcule la energía total disipada en la espira entre 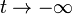$t\to-\infty$ y $t\to+\infty$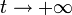

2 Intensidad de corriente

Por la ley de Faraday

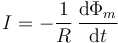
$I=-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}$

Consideramos la intensidad de corriente recorrida en sentido antihorario.

En este caso, tenemos 5 fases.

Antes de que la espira entre en el campo (t<0)

El flujo es constante, ya que es nulo y por tanto

$I=0\,$

Cuando el primer lado entra y antes de que salga ( $0 < t < c / v 0$ )

El flujo aumenta como

$\Phi_m=B_0bx\,$

y por tanto

$I=-\frac{B_0bv_0}{R}\qquad\qquad \left(0<t<\frac{c}{v_0}\right)$

Cuando el primer lado ha salido, y el segundo aun no ha entrado ( $c / v 0 < t < b / v 0$ )

El flujo es constante e igual agente

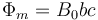
$\Phi_m = B_0bc\,$

y por tanto

$I=0\qquad\qquad \left(\frac{c}{v_0}<t<\frac{b}{v_0}\right)$

Cuando el segundo lado antra y antes de que haya salido ( $b / v 0 < t < (c + b) / v 0$ )

El flujo disminuye al mismo ritmo que antes aumentaba. Por tanto

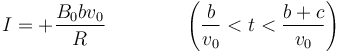
$I=+\frac{B_0bv_0}{R}\qquad\qquad \left(\frac{b}{v_0}<t<\frac{b+c}{v_0}\right)$

Cuando la espira sale del todo ( $t > (b + c) / v 0$ )

El flujo vuelve a ser nulo y

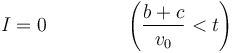
$I=0 \qquad\qquad\left(\frac{b+c}{v_0}<t\right)$

Resumiendo

$I(t)=\frac{B_0bv_0}{R}\begin{cases} 0 & t < 0 \\ -1& 0 < t < c/v_0 \\ 0 & c/V_0 < t < b/v_0 \\ +1 & b/v_0 < t < (b+c)/v_0 \\ 0 & t < (b+c)/v_0\end{cases}$

Espira que entra en una franja campo magnético (GIE)

De Laplace

Contenido

1 Enunciado

2 Intensidad de corriente

3 Potencia disipada

4 Fuerza sobre la espira

5 Potencia mecánica

6 Energía total disipada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES