Espira que entra en una franja campo magnético (GIE)

De Laplace

Contenido

1 Enunciado
2 Intensidad de corriente
3 Potencia disipada
4 Fuerza sobre la espira
5 Potencia mecánica
6 Energía total disipada

1 Enunciado

Una espira cuadrada de lado $b$ y resistencia eléctrica $R$ se encuentra en el plano $z = 0$ con lados paralelos a los ejes. La espira se halla inmersa en un campo magnético dependiente de la posición como

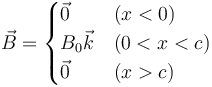
$\vec{B}=\begin{cases}\vec{0} & (x<0) \\ B_0\vec{k} & (0<x<c) \\ \vec{0} & (x>c)\end{cases}$

siendo $c$ una constante que cumple $c < b$ . La espira es obligada a moverse con velocidad constante 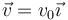$\vec{v}=v_0\vec{\imath}$ . En $t = 0$ el lado delantero de la espira se halla en $x = 0$ .

Determine, como función del tiempo:

La intensidad de corriente inducida en la espira.
La potencia disipada por efecto Joule.
La fuerza magnética sobre la espira.
La potencia mecánica sobre la espira debida al agente que mantiene la espira con velocidad constante.
Calcule la energía total disipada en la espira entre 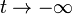$t\to-\infty$ y $t\to+\infty$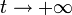

2 Intensidad de corriente

Por la ley de Faraday

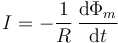
$I=-\frac{1}{R}\,\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}$

Consideramos la intensidad de corriente recorrida en sentido antihorario.

En este caso, tenemos 5 fases.

Antes de que la espira entre en el campo.
Cuando el primer lado entra y antes de que salga
Cuando el primer lado ha salido, y el segundo aun no ha entrado
Cuando el segundo lado entra y antes de que haya salido
Cuando la espira ya ha salido del todo

En los pasos 1, 3 y 5 el flujo magnético es constante, por lo que la intensidad de corriente es nula.

En la fase 2 el flujo aumenta como

$\Phi_m=B_0bx\,$

y por tanto

$I=-\frac{B_0bv_0}{R}\qquad\qquad \left(0<t<\frac{c}{v_0}\right)$

En la fase 4, el flujo disminuye al mismo ritmo que antes aumentaba, por lo que la corriente es de la misma magnitud y sentido opuesto.

La duración del intervalo 2 y la del 4 es lo que tarda la espira en recorrer una distanciac, esto es $T 2 = T 4 = c / v 0$ .

La duración del intervalo 3 es lo que tarda la espira en recorrer una distancia (b-c), $T 3 = (b - c) / v 0$

Resumiendo

$I(t)=\frac{B_0bv_0}{R}\begin{cases} 0 & t < 0 \\ -1& 0 < t < c/v_0 \\ 0 & c/v_0 < t < b/v_0 \\ +1 & b/v_0 < t < (b+c)/v_0 \\ 0 & t < (b+c)/v_0\end{cases}$

Gráficamente, esta función está formada por una serie de escalones

3 Potencia disipada

La potencia disipada en cada instante es, por la ley de Joule

$P=I^2R=\frac{(B_0bv_0)^2}{R}\begin{cases} 0 & t < 0 \\ +1& 0 < t < c/v_0 \\ 0 & c/v_0 < t < b/v_0 \\ +1 & b/v_0 < t < (b+c)/v_0 \\ 0 & t < (b+c)/v_0\end{cases}$

Esta potencia es nu nula salvo en los intervalos en que la espira entra o sale del campo magnético.

Gráficamente, de nuevo resultan escalones, aunque la potencia es siempre positiva (o nula).

El área bajo la curva es la energía total disipada por efeco Joule, que se calcula más tarde.

4 Fuerza sobre la espira

La fuerza magnética es nula cuando la intensidad de corriente lo sea.

Cuando la intensidad es distinta de 0, la fuerza sobre una espira parcialmente inmersa en un campo magnético es

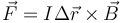
$\vec{F} = I \Delta \vec{r}\times \vec{B}$

con 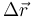$\Delta \vec{r}$ el vector que va desde el punto en que la espira entra en el campo hasta el punto en que sale de él. Este vector vale 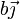$b\vec{\jmath}$ cuando entra el primer lado y $-b\vec{\jmath}$ cuando entra el lado posterior. Por tanto la fuerza es

$\vec{F}_m=-\frac{(B_0b)^2v_0}{R}\vec{\imath}\begin{cases} 0 & t < 0 \\ +1& 0 < t < c/v_0 \\ 0 & c/v_0 < t < b/v_0 \\ +1 & b/v_0 < t < (b+c)/v_0 \\ 0 & t < (b+c)/v_0\end{cases}$

5 Potencia mecánica

Para mantener una velocidad constante, es necesario aplicar una fuerza opuesta a la anterior

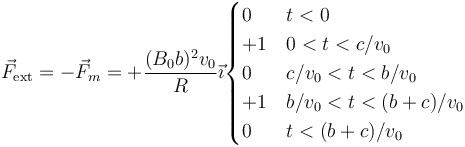
$\vec{F}_\mathrm{ext}=-\vec{F}_m=+\frac{(B_0b)^2v_0}{R}\vec{\imath}\begin{cases} 0 & t < 0 \\ +1& 0 < t < c/v_0 \\ 0 & c/v_0 < t < b/v_0 \\ +1 & b/v_0 < t < (b+c)/v_0 \\ 0 & t < (b+c)/v_0\end{cases}$

La potencia desarrollada por esta fuerza es

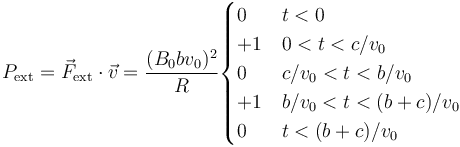
$P_\mathrm{ext}=\vec{F}_\mathrm{ext}\cdot\vec{v}=\frac{(B_0bv_0)^2}{R}\begin{cases} 0 & t < 0 \\ +1& 0 < t < c/v_0 \\ 0 & c/v_0 < t < b/v_0 \\ +1 & b/v_0 < t < (b+c)/v_0 \\ 0 & t < (b+c)/v_0\end{cases}$

que es igual a la calculada antes.

6 Energía total disipada

La potencia es no nula en dos intervalos de duración $c / v 0$ . En esos intervalos la potencia es constante. Por tanto, la energía total disipada es

$W_d=\int_{-\infty}^\infty P\,\mathrm{d}t=2\frac{(B_0bv_0)^2}{R}\frac{c}{v_0}=\frac{2B_0^2b^2cv_0}{R}$

Espira que entra en una franja campo magnético (GIE)

De Laplace

Contenido

1 Enunciado

2 Intensidad de corriente

3 Potencia disipada

4 Fuerza sobre la espira

5 Potencia mecánica

6 Energía total disipada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES