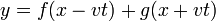Deducción de la ecuación de onda en una dimensión
De Laplace
Contenido |
1 Objetivo
Nuestro objetivo es hallar la ecuación diferencial que deben verificar las soluciones para las ondas en una dimensión. Debe cumplir los siguientes requisitos:
2 Ondas hacia la derecha
Debe admitir como soluciones las de la forma
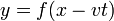
que representan señales que se propagan hacia la derecha sin deformarse.
3 Ondas hacia la izquierda
Una cuerda, u otro sistema vibrante, normalmente es simétrica respecto al sentido de propagación de las ondas. No hay diferencia entre agitar el extremo de la izquierda y producir una onda que se mueve hacia la derecha, que agitar el de la derecha y que la onda resultante se mueva hacia la izquierda.
Por tanto, la ecuación diferencial buscada debe admitir también soluciones de la forma
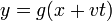
con g una función arbitraria.
4 Superposición
La ecuación resultante debe admitir además que sobre la misma cuerda vibrante se propaguen simultáneamente dos o más señales, sin afectarse mutuamente. Por ello la solución general debe ser de la forma