No Boletín - Area de un polígono (Ex.Oct/17)
De Laplace
1 Enunciado
Sea 
el área del polígono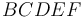 
de la figura adjunta.
¿Cuál de las siguientes igualdades es falsa?
- (1)
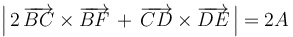
- (2)
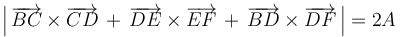
- (3)
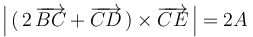
- (4)
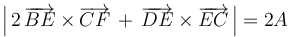
2 Solución
Un detalle importante que conviene observar en las cuatro igualdades propuestas (aplíquese en la (3) la propiedad distributiva respecto a la suma) es que todos los productos vectoriales que aparecen en ellas tienen la misma dirección (perpendicular al plano del polígono) y el mismo sentido (saliente). Nótese que, sólo cuando se suman vectores que tienen la misma dirección y el mismo sentido, se puede igualar el módulo de la suma con la suma de los módulos. Así pues, podemos reescribir las cuatro igualdades propuestas del siguiente modo:
- (1)
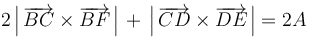
- (2)
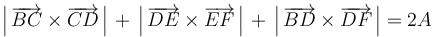
- (3)
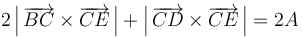
- (4)
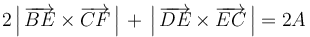
A continuación, vamos a examinar la cuatro igualdades propuestas, pero teniendo en cuenta la propiedad geométrica del producto vectorial que dice que "el módulo del producto vectorial de dos vectores es igual al área del paralelogramo que tiene a ambos vectores como lados", o bien, que "el módulo del producto vectorial de dos vectores es igual al doble del área del triángulo que tiene a ambos vectores como dos de sus lados". Utilizaremos la siguiente notación: una secuencia de letras entre paréntesis a continuación de la palabra "Area" significa el área del polígono que tiene por vértices los puntos representados por esas letras (3 letras para un triángulo, 4 letras para un paralelogramo y 5 letras para el polígono del enunciado).
![\mathrm{(1)}\,\,\,\longrightarrow\,\,\,\underbrace{\underbrace{\underbrace{2\left|\,\overrightarrow{BC}\times\overrightarrow{BF}\,\right|}_{2\,\mathrm{Area}(BCEF)}\,+\,\underbrace{\left|\,\overrightarrow{CD}\times\overrightarrow{DE}\,\right|}_{2\,\mathrm{Area}(CDE)}}_{2\,[\mathrm{Area}(BCEF)\,+\,\mathrm{Area}(CDE)]}}_{2\,\mathrm{Area}(BCDEF)}=2A\,](/wiki/images/math/c/2/c/c2c3b9e22c3bd9482c9912c162631271.png)
![\mathrm{(2)}\,\,\,\longrightarrow\,\,\,\underbrace{\underbrace{\underbrace{\left|\,\overrightarrow{BC}\times\overrightarrow{CD}\,\right|}_{2\,\mathrm{Area}(BCD)}\,+\,\underbrace{\left|\,\overrightarrow{DE}\times\overrightarrow{EF}\,\right|}_{2\,\mathrm{Area}(DEF)}\,+\,\underbrace{\left|\,\overrightarrow{BD}\times\overrightarrow{DF}\,\right|}_{2\,\mathrm{Area}(BDF)}}_{2\,[\mathrm{Area}(BCD)\,+\,\mathrm{Area}(DEF)+\,\mathrm{Area}(BDF)]}}_{2\,\mathrm{Area}(BCDEF)}=2A\,](/wiki/images/math/5/2/5/525c6a2e899862e1ef846f9a6d30fb7b.png)
![\mathrm{(3)}\,\,\,\longrightarrow\,\,\,\underbrace{\underbrace{\underbrace{2\left|\,\overrightarrow{BC}\times\overrightarrow{CE}\,\right|}_{2\,\mathrm{Area}(BCEF)}\,+\,\underbrace{\left|\,\overrightarrow{CD}\times\overrightarrow{CE}\,\right|}_{2\,\mathrm{Area}(CDE)}}_{2\,[\mathrm{Area}(BCEF)\,+\,\mathrm{Area}(CDE)]}}_{2\,\mathrm{Area}(BCDEF)}=2A\,](/wiki/images/math/1/2/b/12b8bb408cc6bbff0d66548ab06620d0.png)
Llegados a este punto, ya hemos comprobado que las igualdades (1), (2) y (3) son correctas. Por tanto, llegamos a la conclusión -por eliminación- de que la igualdad (4) es la que es FALSA.
No obstante, comprobémoslo:
![\mathrm{(4)}\,\,\,\longrightarrow\,\,\,2\left|\,\overrightarrow{BE}\times\overrightarrow{CF}\,\right|\,+\,\left|\,\overrightarrow{DE}\times\overrightarrow{EC}\,\right|=2\left|\,(\overrightarrow{BC}\,+\,\overrightarrow{CE})\times(\overrightarrow{CE}\,+\,\overrightarrow{EF})\,\right|\,+\,\left|\,\overrightarrow{DE}\times\overrightarrow{EC}\,\right|=\underbrace{\underbrace{\underbrace{2\left|\,\overrightarrow{BC}\times\overrightarrow{CE}\,\right|}_{2\,\mathrm{Area}(BCEF)}\,+\,\underbrace{2\left|\,\overrightarrow{BC}\times\overrightarrow{EF}\,\right|}_{\vec{0}}\,+\,\underbrace{2\left|\,\overrightarrow{CE}\times\overrightarrow{CE}\,\right|}_{\vec{0}}\,+\,\underbrace{2\left|\,\overrightarrow{CE}\times\overrightarrow{EF}\,\right|}_{2\,\mathrm{Area}(BCEF)}\,+\,\underbrace{\left|\,\overrightarrow{DE}\times\overrightarrow{EC}\,\right|}_{2\,\mathrm{Area}(CDE)}}_{2\,\mathrm{Area}(BCEF)\,+\,2\,[\mathrm{Area}(BCEF)+\,Area(CDE)]}}_{2\,\mathrm{Area}(BCEF)\,+\,2\,\mathrm{Area}(BCDEF)}\neq 2A\,](/wiki/images/math/8/f/4/8f4c47e6acf31bed7cf49263f17d1bdc.png)
