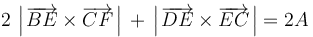No Boletín - Area de un polígono (Ex.Oct/17)
De Laplace
1 Enunciado
Sea  el área del polígono
el área del polígono 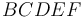 de la figura adjunta.
de la figura adjunta.
¿Cuál de las siguientes igualdades es falsa?
- (1)
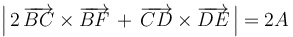
- (2)
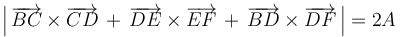
- (3)
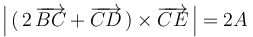
- (4)
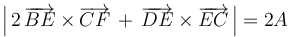
2 Solución
En primer lugar, observamos que todos los productos vectoriales presentes en las cuatro igualdades propuestas (incluidos los dos obtenidos en la tercera igualdad tras aplicar la propiedad distributiva respecto a la suma) tienen la misma dirección y sentido. Este detalle es importante porque nos va a permitir igualar el módulo de cada suma de productos vectoriales con la suma de los módulos de los sumandos. Y es que, aunque en general el módulo de una suma de vectores no es igual a la suma de los módulos de los vectores, dicha igualdad sí que es cierta cuando los vectores sumados tienen todos la misma dirección y el mismo sentido, que es precisamente lo que aquí ocurre: los vectores 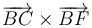 ,
, 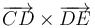 ,
, 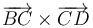 ,
, 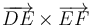 ,
, 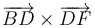 ,
, 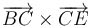 ,
, 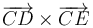 ,
, 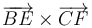 y
y 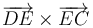 tienen todos dirección perpendicular al plano que contiene al polígono
tienen todos dirección perpendicular al plano que contiene al polígono 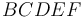 y sentido saliente de dicho plano.
y sentido saliente de dicho plano.
Por tanto, podemos reescribir las cuatro igualdades propuestas del siguiente modo:
- (1)
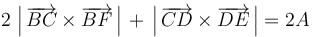
- (2)
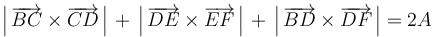
- (3)
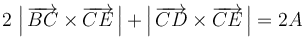
- (4)