No Boletín - Péndulo simple (Ex.Ene/18)

De Laplace

1 Enunciado

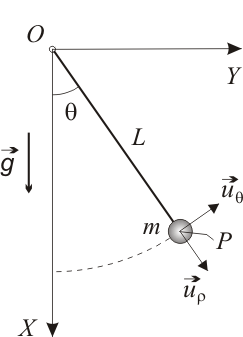
Considérese un péndulo simple, constituido por una partícula (de masa 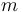) que se halla suspendida de un punto fijo mediante un hilo inextensible (de longitud y masa despreciable). Bajo la acción de su propio peso, la partícula oscila en el plano vertical fijo 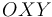(aceleración gravitatoria: 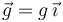). Se propone la coordenada acimutal (definida en la figura) para describir la posición de la partícula , así como la base polar 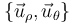para expresar las magnitudes vectoriales.

1. De la segunda ley de Newton aplicada a la partícula y proyectada sobre la dirección acimutal, deduzca la ecuación diferencial de segundo orden que debe satisfacer la función .
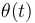2. Y de la misma ley, pero proyectada sobre la dirección radial, deduzca el módulo de la tensión del hilo.
3. Deduzca una integral primera del movimiento de la partícula aplicando algún teorema de conservación.

2 Solución