Percusión sobre un sistema articulado

De Laplace

Revisión a fecha de 12:27 12 feb 2018; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Percusión en OA
4 Percusión en AB

1 Enunciado

Considerando el sistema de dos barras articuladas del problema “dos barras articuladas” suponga que el sistema se halla completamente extendido y en reposo. Entonces, se efectúa una percusión 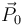$\vec{P}_0$ perpendicular a la dirección de las barras y a una distancia c de la articulación A entre las dos barras.

Determine la velocidad angular de cada barra, así como la velocidad de los puntos A y B (extremo libre de la segunda barra) en los casos:

Se golpea la barra OA en un punto D a una distancia c de la articulación A.
Se golpea la barra AB en un punto D a una distancia c de la articulación A.

2 Introducción

La ecuación básica que gobierna un sistema sometida a percusiones es la de Lagrange

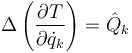
$\Delta\left(\frac{\partial T}{\partial \dot{q}_k}\right)=\hat{Q}_k$

suponiendo coordenadas independientes y siendo 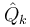$\hat{Q}_k$ la percusión generalizada

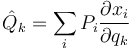
$\hat{Q}_k=\sum_i P_i \frac{\partial x_i}{\partial q_k}$

siendo las $x i$ las coordenadas del punto donde se aplica la percusión.

En nuestro caso el sistema tiene dos grados de libertad, que podemos describir con el ángulo φ que la varilla OA forma con el eje OX y el ϕ que la varilla AB forma con el mismo eje.

En este caso, podemos emplear la energía cinética para el sistema de dos varillas que se describe en el problema citado:

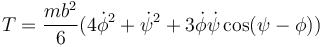
$T=\frac{mb^2}{6}(4\dot{\phi}^2+\dot{\psi}^2+3\dot{\phi}\dot{\psi}\cos(\psi-\phi))$

Sin embargo, tal como se ve en dicho problema, la deducción es un tanto laboriosa y requiere emplear diferentes base vectoriales.

En el caso de una percusión, el cálculo puede simplificarse sustituyendo las coordenadas por los valores que tienen en el momento de la percusión, ya que

Durante una percusión, el intervalo de tiempo es tan corto que no hay lugar a que cambien las coordenadas.
las derivadas que hay que calcular son respecto a las velocidades, con lo que se pueden tratar las coordenadas como constantes.

Teniendo esto en cuenta, hallamos las velocidades instantáneas de los puntos A y B respecto a un sistema fijo

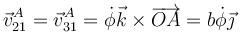
$\vec{v}^A_{21}=\vec{v}^A_{31}=\dot{\phi}\vec{k}\times\overrightarrow{OA}=b\dot{\phi}\vec{\jmath}$

y

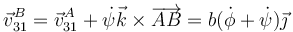
$\vec{v}^B_{31}=\vec{v}^A_{31}+\dot{\psi}\vec{k}\times\overrightarrow{AB}=b(\dot{\phi}+\dot{\psi})\vec{\jmath}$

Obsérvese que no hace falta distinguir qué base vectorial estamos empleando ya que todas son coincidentes en ese instante.

La energía cinética en ese instante es entonces, aplicando la expresión para la energía cinética de una varilla

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): T=\frac{m}{6}|\vec{v}^A_{21}|^2+\frac{m}}{6}\left(|\vec{v}^A_{31}|^2+|\vec{v}^B_{31}|^2+\vec{v}^A_{31}\cdot\vec{v}^B_{31}\right)

Sustituimos las expresiones anteriores y queda

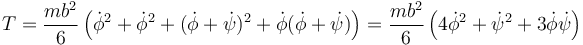
$T=\frac{mb^2}{6}\left(\dot{\phi}^2+\dot{\phi}^2+(\dot{\phi}+\dot{\psi})^2+\dot{\phi}(\dot{\phi}+\dot{\psi})\right)=\frac{mb^2}{6}\left(4\dot{\phi}^2+\dot{\psi}^2+3\dot{\phi}\dot{\psi}\right)$

Este es el mismo resultado al que se llega haciendo $cos(ψ - φ) = 1$ en la expresión general, pero el proceso es más simple.

Derivamos ahora respecto a cada velocidad generalizada y queda para φ

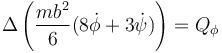
$\Delta \left(\frac{mb^2}{6}(8\dot{\phi}+3\dot{\psi})\right)=Q_\phi$

y para ϕ

$\Delta \left(\frac{mb^2}{6}(3\dot{\phi}+2\dot{\psi})\right)=Q_\phi$

3 Percusión en OA

4 Percusión en AB

Percusión sobre un sistema articulado

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Percusión en OA

4 Percusión en AB

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES