Manivela y biela alargada, Enero 2018 (G.I.E.R.M.)
De Laplace
Contenido |
1 Enunciado
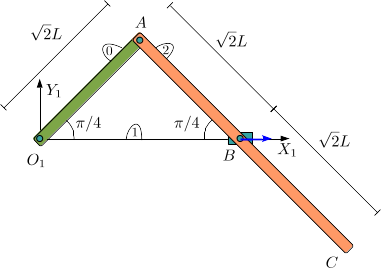
Una barra homogénea (sólido "0") de longitud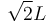 
tiene un extremo articulado en el
punto fijo O. En el otro extremo, A, se articula otra barra homogénea de longitud
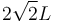(sólido "2"). El punto medio de esta barra se articula a su vez en un pasador
(punto B), de modo que este punto de la barra se mueve sobre el eje O1X1. La barra "0"
gira alrededor del eje O1Z1 con velocidad angular uniforme Ω.
Todas las magnitudes físicas que se piden
corresponden al instante que se muestra en la figura.
- Localiza gráfica y analíticamente los C.I.R. de los tres movimientos relativos que se pueden definir en el sistema.
- Encuentra reducciones cinemáticas de los tres movimientos relativos. Calcula
.
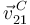- Calcula la derivada temporal de la reducción cinemática del movimiento {21} en el punto B.
2 Solución
2.1 Análisis previo
Del enunciado y la figura podemos deducir la siguiente información cinemática
- Todos los movimientos son planos, por lo que todos los vectores de rotación son paralelos al vector
.
- El punto O1 de la barra "0" es un punto fijo:
.
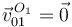- Las barras "2" y "0" están articuladas en el punto A:
.
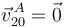- La velocidad de rotación absoluta de la barra "0" es constante:
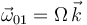y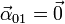 
.
- El punto B de la barra "2" se mueve siempre sobre el eje O1X1:
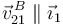y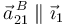 
.
2.2 Localización de los C.I.R.
Del análisis previo deducimos inmediatamente
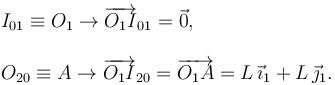
Para encontrar I21 usamos primero que 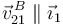. Entonces I21 debe estar en la línea perpendicular a 
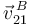trazada por B. Por otro lado, por el Teorema de los Tres Centros, I21 debe estar también el la línea que une I01 y I20. El corte de las dos líneas
da la posición de I21. Como se observa en la figura tenemos
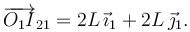
Hemos usado que todos los triángulos son rectángulos e isósceles.
2.3 Reducciones cinemáticas
2.3.1 Movimiento {01}
Del análisis previo obtenemos inmediatamente
2.3.2 Movimiento {20}
Del análisis previo obtenemos 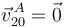, pero no sabemos el vector rotación. Sólo
sabemos que podemos escribirlo como
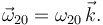
2.3.3 Movimiento {21}
En este punto sólo podemos escribir esto
Usando la composición {21} = {20} + {01} podemos calcular 
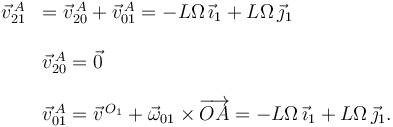
El vector 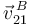puede calcularse también usando la ecuación del campo de
velocidades del movimiento {21}
