Problemas de mecánica analítica (CMR)

De Laplace

1 Estudio analítico de máquina de Atwood

Una máquina de Atwood está formada por dos masas m₁ y No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): m_ 2 unidas por un hilo ideal, inextensible y sin masa, que pasa por una polea ideal, sin rozamiento y sin masa.

1. Empleando el principio de D’Alembert halle la aceleración de cada una de las masas.
2. Con ayuda de los multiplicadores de Lagrange, calcule la tensión del hilo que pasa por la polea.
3. Suponga ahora que la polea es un disco de radio R con momento de inercia I. ¿Cómo queda en ese caso la aceleración de las masas? ¿Y las tensiones de la cuerda?

2 Estudio analítico del plano inclinado

Una partícula de masa m desliza sin rozamiento por un plano inclinado, de base b y altura h, sometida a la fuerza de la gravedad y las fuerzas de reacción. Empleando como coordenadas las cartesianas de la partícula con el eje OX horizontal y el OY vertical:

1. Escriba la ecuación del vínculo entre las coordenadas.
2. A partir del principio de D’Alembert, obtenga las componentes de la aceleración de la masa.
3. Con ayuda de los multiplicadores de Lagrange, halle las componentes de la fuerza de reacción del plano sobre la masa.

3 Estudio analítico del péndulo simple

Empleando el principio de D’Alembert, obtenga las ecuaciones de movimiento para las coordenadas cartesianas de un péndulo simple que oscila verticalmente.

4 Estudio analítico de dos masas unidas por un muelle

Como en el problema “Dos masas unidas por un muelle” tenemos dos masas m₁ y m₂ se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura 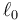. Inicialmente las dos masas se encuentran en reposo en x₁₀ = 0 y 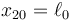. Entonces se le comunica a la masa m₁ una velocidad v₀ en el sentido positivo del eje.

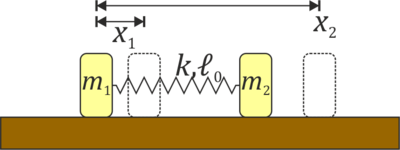
1. Determine la lagrangiana del sistema en función de las posiciones de las dos partículas.
2. Obtenga las ecuaciones de movimiento para x₁ y x₂

Realice el cambio de variables a las coordenadas generalizadas x_G = (m₁x₁ + m₂x₂) / (m₁ + m₂), .

3. ¿Cómo queda la lagrangiana en función de estas coordenadas?
4. Obtenga las ecuaciones de movimiento para x_G y x.
5. Determine dos constantes de movimiento para este sistema.

5 Estudio analítico de una barra apoyada

Como en el problema “Barra deslizante con masas en los extremos”, supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies

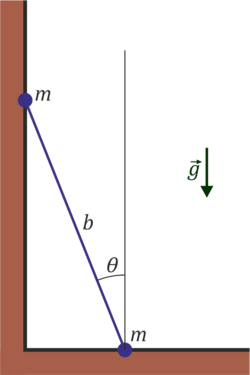
1. Determine la lagrangiana del sistema.
2. Halle la ecuación de movimiento para el ángulo θ.
3. Determine una constante de movimiento no trivial.
4. Añadiendo una coordenada x que representaría la separación de la barra respecto de la pared vertical, calcule la fuerza de reacción ejercida por la pared.
5. Existe un valor de θ para el cual la barra se separa de la pared. Determine este valor.
6. Halle la ecuación de movimiento para la barra una vez que se ha separado de la pared.

6 Péndulo compuesto

Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.

Para este sistema

1. Calcule la lagrangiana del sistema.
2. Halle las ecuaciones de movimiento para los dos ángulos de giro, θ y ϕ
3. Obtenga dos constantes de movimiento no triviales.
4. Con ayuda de las constantes de movimiento, halle una ecuación que incluya solamente a θ
5. Calcule el valor que debe tener la velocidad angular 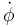si se desea que la barra mantenga una inclinación constante respecto a la vertical.

7 Dos barras articuladas

Un sistema está formado por dos varillas homogéneas, ambas de masa m y longitud b, situadas sobre un plano horizontal (“sólido 1”). La varilla “2” está articulada por su extremo O a un punto fijo del plano, mientras que por su extremo A está articulada a la varilla “3”.

1. Escriba la lagrangiana del sistema, empleando como coordenadas generalizadas los ángulos que ambas varillas forman con el eje OX.
2. Obtenga las ecuaciones de movimiento para estos dos ángulos.
3. ¿Es cíclica alguna de estas coordenadas?

Si en lugar de esas coordenadas se usan el ángulo ϕ que la varilla OA forma con OX y el ángulo θ que AB forma con la prolongación de OA

4. ¿Cómo queda la lagrangiana?
5. ¿Y las ecuaciones de movimiento para estos ángulos?
6. ¿Es cíclica alguna de estas coordenadas?
7. Determine dos constantes de movimiento para este sistema.
8. Con ayuda de estas constantes, reduzca el problema a una única ecuación de movimiento para el ángulo θ.

Suponga ahora que la varilla 2 es forzada a girar con velocidad angular constante Ω en torno a O.

9. Escriba la lagrangiana para este sistema en función del ángulo θ.
10. Obtenga la ecuación de movimiento para θ. ¿Es la misma que en el apartado (8)?
11. ¿Se conserva la energía en este sistema? ¿Hay alguna otra constante de movimiento?

8 Estudio analítico de una partícula dentro de un tubo

Una partícula de masa m se encuentra en el interior de un tubo estrecho, el cual se halla en todo momento contenido en el plano OXY girando con velocidad angular Ω constante alrededor del eje OZ

1. Determine la lagrangiana de este sistema.
2. Halle la ecuación de movimiento para la coordenada radial ρ.
3. ¿Se conserva la energía en este sistema? Si no es así, ¿hay alguna otra magnitud similar que sí se conserve?
4. Con ayuda de los multiplicadores de Lagrange, calcule la fuerza de reacción generalizada que el tubo ejerce sobre la partícula.