Estudio analítico de dos masas unidas por un muelle

De Laplace

1 Enunciado

Como en el problema “Dos masas unidas por un muelle” tenemos dos masas m₁ y m₂ se mueven a lo largo del eje OX unidas por un resorte de constante k y longitud natura 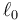. Inicialmente las dos masas se encuentran en reposo en x₁₀ = 0 y 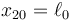. Entonces se le comunica a la masa m₁ una velocidad v₀ en el sentido positivo del eje.

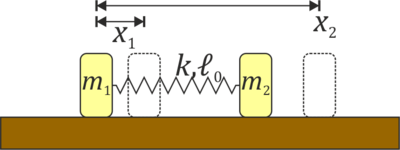
1. Determine la lagrangiana del sistema en función de las posiciones de las dos partículas.
2. Obtenga las ecuaciones de movimiento para x₁ y x₂

Realice el cambio de variables a las coordenadas generalizadas x_G = (m₁x₁ + m₂x₂) / (m₁ + m₂), .

3. ¿Cómo queda la lagrangiana en función de estas coordenadas?
4. Obtenga las ecuaciones de movimiento para x_G y x.
5. Determine dos constantes de movimiento para este sistema.

2 Lagrangiana en función de x₁ y x₂

3 Ecuaciones de movimiento para x₁ y x₂

4 Lagrangiana en función de x y x_G

5 Ecuaciones de movimiento para x y x_G

6 Constantes de movimiento