Dos masas unidas por un péndulo

De Laplace

Enunciado

Dos masas de valor m₁ y m₂ se encuentran unidas por una varilla rígida de longitud b y masa despreciable. m₁ puede deslizarse sin rozamiento sobre una superficie horizontal, mientras que m₂ cuelga de la varilla pudiendo oscilar y moverse en el plano OXZ. Todo el sistema está sometido a la acción del peso.

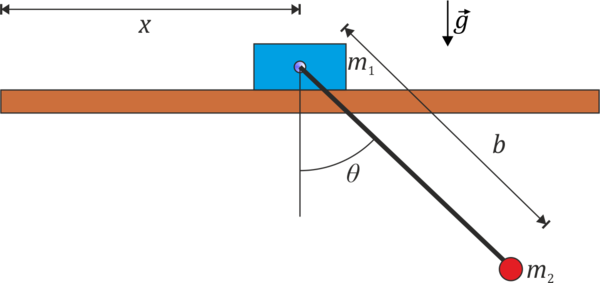
1. Empleando los procedimientos de la dinámica vectorial (es decir, considerando todas las fuerzas que actúan sobre cada masa), determine las ecuaciones de movimiento para las dos masas, en función del ángulo con la vertical θ y de la posición x de la masa m₁.
2. Determine dos constantes de movimiento en este problema. ¿Qué representan físicamente?
3. Suponga que estando el péndulo vertical se aguanta la masa superior y la inferior se separa de la vertical un pequeño ángulo θ₀.
   1. ¿A qué se reducen las ecuaciones de movimiento en ese límite θ≪1?
   2. ¿Cuál es la frecuencia de oscilación? ¿A qué tiende en los casos m_1→∞ y m_1→m_2?
4. Suponga que se sube la masa 2 hasta que el péndulo queda horizontal. Estando las dos masas en reposo, se suelta m₂. Para el momento en que el péndulo pasa por la posición vertical
   1. ¿Cuál es la rapidez de m₂? ¿Y de m₁?
   2. ¿Cuánto vale la tensión de la barra?
   3. ¿Cuánto vale la fuerza de reacción normal del plano que sostiene a m₁?