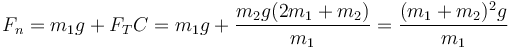Dos masas unidas por un péndulo
De Laplace
Contenido |
1 Enunciado
Dos masas de valor m1 y m2 se encuentran unidas por una varilla rígida de longitud b y masa despreciable. m1 puede deslizarse sin rozamiento sobre una superficie horizontal, mientras que m2 cuelga de la varilla pudiendo oscilar y moverse en el plano OXZ. Todo el sistema está sometido a la acción del peso.
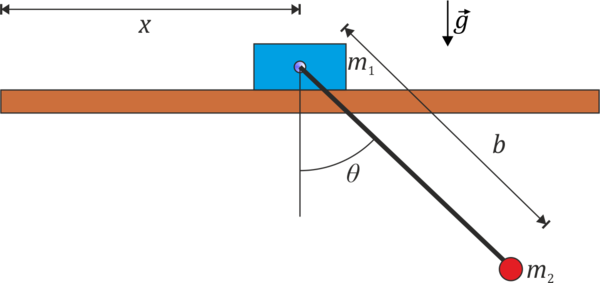
- Empleando los procedimientos de la dinámica vectorial (es decir, considerando todas las fuerzas que actúan sobre cada masa), determine las ecuaciones de movimiento para las dos masas, en función del ángulo con la vertical θ y de la posición x de la masa m1.
- Determine dos constantes de movimiento en este problema. ¿Qué representan físicamente?
- Suponga que estando el péndulo vertical se aguanta la masa superior y la inferior se separa de la vertical un pequeño ángulo θ0.
- ¿A qué se reducen las ecuaciones de movimiento en ese límite θ≪1?
- ¿Cuál es la frecuencia de oscilación? ¿A qué tiende en los casos m_1→∞ y m_1→m_2?
- Suponga que se sube la masa 2 hasta que el péndulo queda horizontal. Estando las dos masas en reposo, se suelta m2. Para el momento en que el péndulo pasa por la posición vertical
- ¿Cuál es la rapidez de m2? ¿Y de m1?
- ¿Cuánto vale la tensión de la barra?
- ¿Cuánto vale la fuerza de reacción normal del plano que sostiene a m1?
2 Ecuaciones de movimiento
En lo que sigue, dada la frecuencia con que aparecerán las funciones trigonométricas, emplearemos las abreviaturas

Se trata de determinar las ecuaciones de movimiento para las dos partículas.
Este sistema posee dos grados de libertad, ya que está sometido a 4 vínculos:
- El movimiento es plano y ambas partículas se mueven en el plano OXY

- La partícula 1 está obligada a moverse sobre una recta horziontal
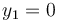
- Las partículas están unidas por una barra rígida
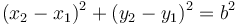
En este caso, todos los vínculos son geométricos, lo que nos permite reducir el sistema a solo dos variables. Empleando las indicadas en el enunciado queda, para la partícula 1

y para la 2

Las componentes de la velocidad y de la aceleración de la primera valen

y las de la segunda
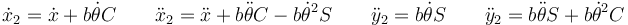
2.1 Para la partícula 1
La partícula está sometida a
- Su peso

- La reacción normal de la superficie de apoyo, normal a ésta
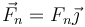
- La tensión de la varilla, que va a lo largo de ella

Separando por componentes queda
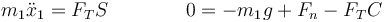
La última ecuación nos permite hallar la reacción normal, que es superior al peso
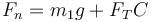
No conocemos la tensión. Pare llo, necesitamos la ecuación de movimiento de la segunda partícula
2.2 Para la partícula 2
La partícula 2 está sometida a
- Su peso
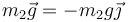
- La tensión de la varilla, que va a lo largo de ella y es opuesta a la que actúa sobre la 1
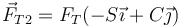
Separando por componentes queda

2.3 Movimiento horizontal del CM
Para la componente horizontal de las dos partículas tenemos que

de donde
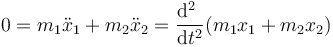
Esta ecuación se puede integrar de forma inmediata
En términos de la posición del centro de masas queda
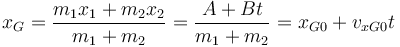
que nos dice que el movimiento horizontal del CM es uniforme. En particular si inicialmente las dos partículas están en reposo, la componente x de la posición del CM permanece constante (aunque el CM se moverá verticalmente).
En términos de la coordenada x de la primera partícula y del ángulo con la vertical, la posición horizontal del CM cumple
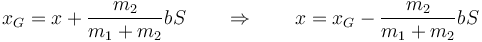
con lo cual, si determinamos como varía en el tiempo el ángulo θ obtenemos también el valor de x como función del tiempo.
2.4 Ecuación para el ángulo θ
Tenemos las dos ecuaciones

Eliminamos la tensión de estas ecuaciones combinándolas y queda

Debemos escribir estas dos derivadas en función del ángulo θ y sus derivadas.
Para 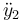 ya lo hemos escrito:
ya lo hemos escrito:
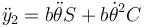
Para 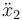 nos ayudamos del CM
nos ayudamos del CM
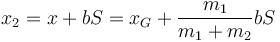
Derivando aquí dos veces

y por tanto llegamos a la ecuación

Agrupamos términos y queda
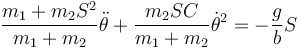
Esta es la ecuación de movimiento para el péndulo. Como vemos es bastante más compleja que para un péndulo simple.
En el caso particular 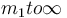 la masa superior se queda inmóvil y la ecuación se reduce a
la masa superior se queda inmóvil y la ecuación se reduce a

que sí es la ecuación del péndulo simple.
3 Constantes de movimiento
Este sistema posee dos integrales primeras o constantes de movimiento (además de las triviales, como las masas o las coordenadas que están fijadas por los vínculos).
3.1 Componente de la cantidad de movimiento
La primera de las dos constantes ya la hemos visto. Se trata de la componente horizontal de la cantidad de movimiento del sistema
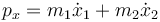
Es la constancia de esta magnitud la que nos da que el movimiento horizontal del CM es uniforme.
En función de x y del ángulo θ esta cantidad vale
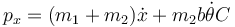
y en función de la posición del CM
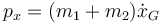
3.2 Energía mecánica
En este sistema todas las fuerzas de reacción vincular son debidas a ligaduras lisas geométricas y esclerónomas, por lo que no realizan trabajo. La única fuerza que sí realiza trabajo es el peso, que es una fuerza conservativa. Por ello, se conserva la energía mecánica del sistema.
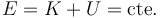
En función de x y del ángulo θ la energía potencial vale

y la cinética
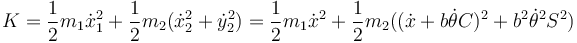
Agrupando términos
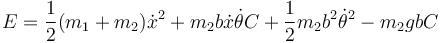
Si en lugar de la coordenada x de la primera partícula empleamos la del CM, la energía cinética queda en la forma
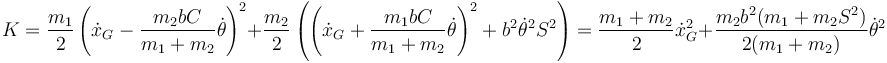
y la mecánica
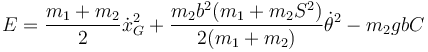
Estas dos constantes de movimiento pueden combinarse. El primero de los sumandos ya es constante por la otra integral primera, por lo que podemos definir una energía mecánica efectiva, también constante, que depende solo del ángulo θ y sus derivadas
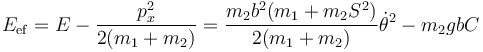
Si derivamos esta cantidad respecto al tiempo reobtenemos la ecuación de movimiento para el ángulo θ. Equivalentemente, integrando dicha ecuación de movimiento se llega a esta integral primera.
4 Pequeñas oscilaciones
Cuando el péndulo está casi vertical y se suelta realiza oscilaciones alrededor de la posición vertical. La frecuencia de etas oscilaciones, no obstante, no es la misma que la de un péndulo simple.
Si 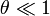 podemos hacer las aproximaciones
podemos hacer las aproximaciones

y despreciar todos los términos en que θ aparezca al cuadrado o potencias superiores. En este caso, la ecuación de movimiento para el ángulo se aproxima a
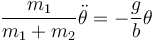
que se transforma en la del oscilador armónico

siendo la frecuencia de las oscilaciones
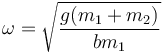
Solo en el límite 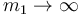 se reduce a la frecuencia del péndulo simple.
se reduce a la frecuencia del péndulo simple.
5 Paso por la vertical
5.1 Velocidades
Si el péndulo se suelta desde el reposo en la posición horizontal quiere decir que las dos constantes de movimiento valen
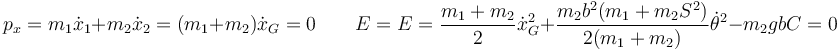
ya que se anulan todos los términos.
La velocidad de la masa 1 cuando el péndulo pasa por la vertical es

y la de la 2
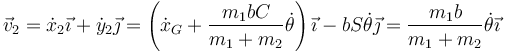
Para completar el cálculo debemos conocer la velocidad angular del péndulo. Obtenemos este valor a partir de la energía mecánica.
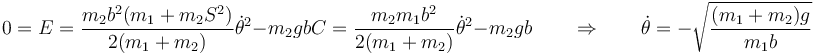
y por tanto

5.2 Tensión de la barra
La tensión de la barra la obtenemos de la ecuación de movimiento para la masa 2. En la posición vertical
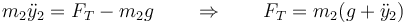
siendo la aceleración vertical de la masa 2 en ese punto (S = 0, C = 1)

El valor de la velocidad angular lo calculamos en el apartado anterior
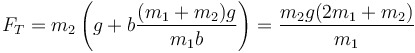
5.3 Reacción del eje horizontal
De la misma manera se calcula la reacción que ejerce el plano sobre el que se halla la masa 1