Problemas de cinemática del movimiento relativo (CMR)

De Laplace

1 Peonza rodante

Una peonza está formada por una varilla de longitud 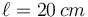ensartada en un disco de radio 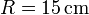. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez 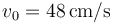. El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula.

Para este movimiento, determine, en el instante en que A se encuentra sobre el eje OX:

1. La velocidad angular del sólido.
2. La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en 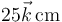, considerado como punto del sólido.
3. La aceleración angular del sólido.
4. La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido.

2 Disco en varilla horizontal

Un disco de radio R (“sólido 2”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 0”). Este eje está montado sobre un soporte vertical fijo de altura R. El disco rueda sin deslizar sobre la superficie horizontal z = 0 (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje OX₀ es a lo largo de la barra horizontal y OZ₀ = OZ₁ en todo momento. Sea (t) el ángulo que el eje OX₀ forma con el OX₁. En un instante dado θ = 0,,.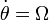

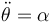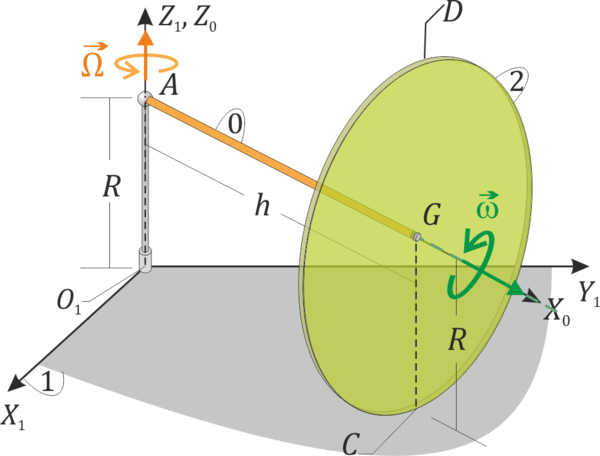
Para ese instante:

1. Determine los vectores , y .
2. Halle la posición de los ejes instantáneos de rotación en los movimientos {01}, {20} y {21}.
3. Calcule las velocidades en el movimiento {21} y el {20} del punto C de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco.
4. Halle las aceleraciones angulares 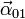, 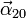y .
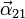5. Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3).

3 Bola que rueda en carril

Una bola (sólido “2”), de radio 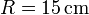, se desplaza sobre dos carriles circulares concéntricos fijos (sólido “1”), de radios 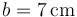y 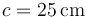, situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que en todo instante, rueda sin deslizar sobre ambos raíles.

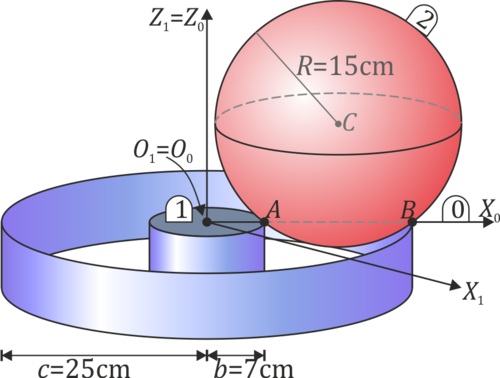
Consideramos como sólido móvil intermedio (sólido 0) al plano O₁X₀Z₀ que contiene en todo instante al centro C de la esfera (ver figura).

1. ¿Cuántos grados de libertad tiene este sistema?
2. Sea θ(t) el ángulo que forma el eje OX₀ con el OX₁. Con ayuda del sólido intermedio halle los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
3. Halle las velocidades angulares y aceleraciones angulares de los movimientos {21}, {20} y {01}
4. Para el punto de la bola en contacto con el carril de mayor radio (punto B), determine 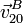y .