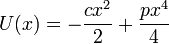Oscilador no lineal

De Laplace

1 Enunciado

Una partícula está sometida exclusivamente a una fuerza, dependiente de la posición, dada por

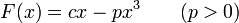
1. Halle la expresión de la energía potencial y la energía mecánica para la partícula. Esboce las gráficas para los casos c < 0 y c > 0.
2. Demuestre que el movimiento de la partícula siempre es acotado, y periódico.
3. Localice las posiciones de equilibrio de la partícula (a) si c < 0 (b) si c > 0.
4. Suponga que la partícula se suelta desde una posición muy próxima a las posiciones de equilibrio calculadas en el apartado anterior. ¿En qué caso describe oscilaciones? Halle el valor aproximado del periodo de oscilación para este movimiento.

2 Solución

2.1 Energía mecánica

Esta fuerza, dependiente solo de la posición, es una fuerza conservativa, que deriva de una energía potencial. Podemos calcular esta energía observando que el trabajo realizado por esta fuerza corresponde a una disminución de la energía potencial

        

Hallando la integral obtenemos la energía potencial

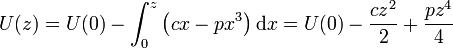
Si tomamos como origen de energía potencial el centro del sistema (z=0) nos queda finalmente,

2.2 Movimiento periódico

2.3 Puntos de equilibrio

2.4 Pequeñas oscilaciones