No Boletín - Area de un triángulo (Ex.Nov/16)
De Laplace
Revisión a fecha de 13:14 2 mar 2017; Enrique (Discusión | contribuciones)
1 Enunciado
Sea 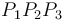 un triángulo de área
un triángulo de área  , y sea
, y sea  un punto coplanario con dicho triángulo e interior al mismo.
un punto coplanario con dicho triángulo e interior al mismo.
¿Cuál de las siguientes igualdades es falsa?
- (1)
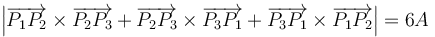
- (2)
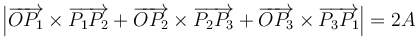
- (3)
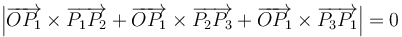
- (4)
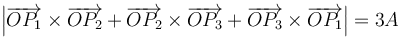
2 Solución
Examinamos en primer lugar la igualdad (3), sacando como factor común de la suma el vector 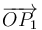 :
:






