Entrar Página Discusión Historial Go to the site toolbox

Disco que rueda sobre corona (GIE)

De Laplace

Revisión a fecha de 15:41 23 ene 2017; Antonio (Discusión | contribuciones)
(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado

Un engranaje está formado por una cavidad circular de radio R (“sólido 1”) que se encuentra inmóvil y por cuyo perímetro interior rueda sin deslizar un disco homogéneo de masa m y radio r (sólido 2). Este disco está empujado por una varilla ideal sin masa cuyo extremo O está engranado a un eje de un motor y que está ranurada de manera que el disco 2 se halla ensartado son rozamiento en la ranura mediante un pequeño vástago de masa despreciable. Todo el sistema es horizontal por lo que no hace falta considerar el efecto del peso. Considere un instante en el que el centro del disco se encuentra sobre el eje OY (ver figura). En ese instante la velocidad del centro G del disco 2 vale No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{v}_G=v_0\vec{\inath} 

y su aceleración tangencial vale a_t=\mathrm{d}|\vec{v}_G|/\mathrm{d}t=a_0.

Para ese instante y empleando el sistema de ejes indicado en la figura (con OZ hacia afuera del papel), halle:

  1. El vector velocidad angular y el vector aceleración angular del disco 2, de radio r.
  2. La aceleración del centro del disco 2 y la del punto A del disco 2 en contacto con el sólido 1.
  3. La energía cinética del disco 2, así como su momento cinético respecto a su centro y respecto al punto O, centro del sistema.
  4. Calcule las fuerzas que se ejercen sobre el disco 2 en su centro (por la varilla) y en el punto A.
  5. Halle el par que ejerce el motor en O para mantener el sistema en funcionamiento.

2 Velocidad y aceleración angulares

2.1 Velocidad angular

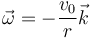
\vec{\omega}=-\frac{v_0}{r}\vec{k}

2.2 Aceleración angular

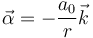
\vec{\alpha}=-\frac{a_0}{r}\vec{k}

3 Aceleraciones

3.1 Del centro de masas

\vec{a}_G = a_0\vec{\imath}+\frac{v_0^2}{R-r}\vec{\jmath}

3.2 Del punto A

\vec{a}_A = \left(\frac{v_0^2}{R-r}+\frac{v_0^2}{r}\right)\vec{\jmath}=\frac{v_0^2R}{r(R-r)}\vec{\jmath}

4 Energía y momentos cinéticos

4.1 Energía cinética

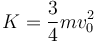
K=\frac{3}{4}m v_0^2

4.2 Momento cinético respecto al CM

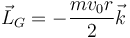
\vec{L}_G=-\frac{mv_0r}{2}\vec{k}

4.3 Momento cinético respecto al punto O

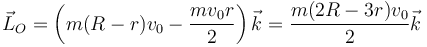
\vec{L}_O=\left(m(R-r)v_0-\frac{mv_0r}{2}\right)\vec{k}=\frac{m(2R-3r)v_0}{2}\vec{k}

5 Fuerzas

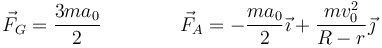
\vec{F}_G=\frac{3ma_0}{2}\qquad\qquad \vec{F}_A=-\frac{ma_0}{2}\vec{\imath}+\frac{mv_0^2}{R-r}\vec{\jmath}

6 Par

\vec{M}_O=\overrightarrow{OG}\times\vec{F}_G=\frac{3ma_0(R-r)}{2}\vec{k}
Obtenido de "http://tesla.us.es/wiki/index.php/Disco_que_rueda_sobre_corona_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace